10 Out Of 60 As A Percentage
listenit
May 26, 2025 · 6 min read
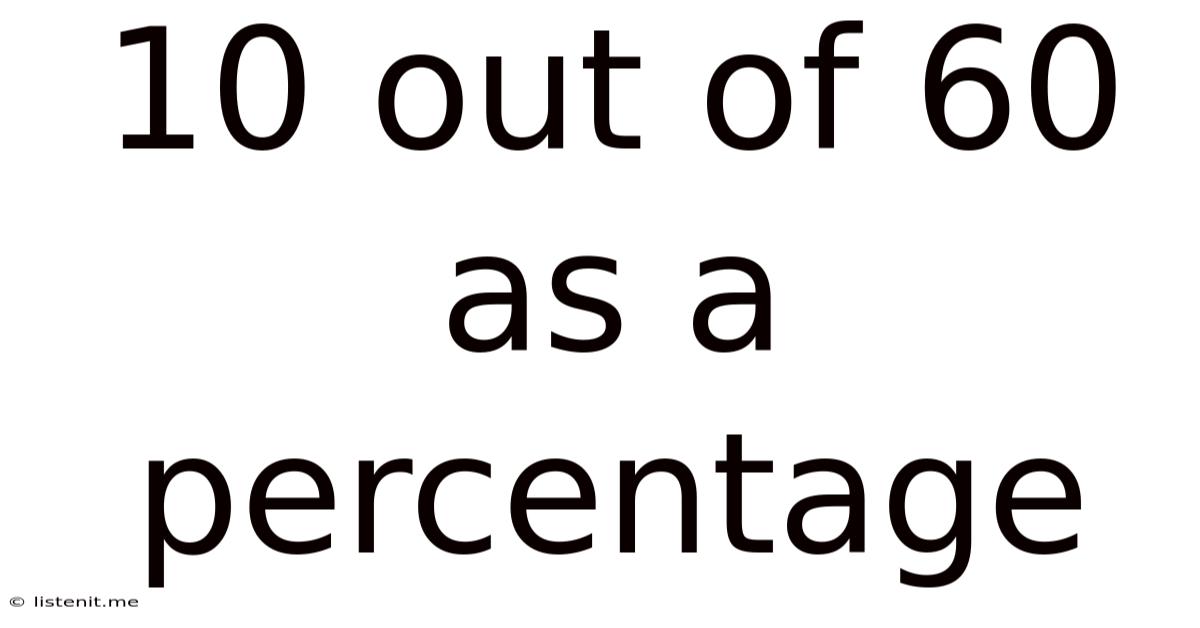
Table of Contents
Decoding the Percentage: 10 out of 60 as a Percentage and its Applications
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex financial analysis. This article delves into the calculation and applications of converting fractions, like 10 out of 60, into percentages. We'll explore the step-by-step process, provide practical examples, and examine the broader implications of percentage calculations.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." It's a convenient method to compare proportions, represent changes, and communicate data effectively. For instance, a score of 85% on a test indicates that you answered 85 out of 100 questions correctly.
Calculating 10 out of 60 as a Percentage
The process of calculating a percentage from a fraction involves a simple two-step method:
Step 1: Convert the fraction to a decimal.
To do this, divide the numerator (the top number) by the denominator (the bottom number):
10 ÷ 60 = 0.166666...
Step 2: Convert the decimal to a percentage.
Multiply the decimal by 100 and add the percent symbol (%):
0.166666... × 100 = 16.67% (rounded to two decimal places)
Therefore, 10 out of 60 is equal to 16.67%.
Understanding the Rounding
Note that the decimal 0.166666... is a recurring decimal. For practical purposes, we typically round the percentage to a manageable number of decimal places. Rounding to two decimal places gives us 16.67%. The level of precision needed will depend on the context. In some cases, rounding to the nearest whole number (17%) might be sufficient.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is crucial in many areas of life:
1. Academics:
- Grade Calculation: Percentages are used extensively to calculate grades based on scores obtained in exams and assignments. For example, if a student scores 45 out of 60 on a test, their percentage score is 75% (45/60 x 100).
- Assessment of Progress: Progress in academic learning is often tracked and represented using percentages, enabling educators and students to monitor performance over time.
2. Finance:
- Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding percentage calculations is essential for making informed financial decisions.
- Discounts and Sales: Sales and discounts are often advertised as percentages (e.g., "20% off"). Calculating the actual price reduction requires converting the percentage to a decimal and applying it to the original price.
- Tax Calculations: Sales tax, income tax, and other taxes are typically calculated as a percentage of the relevant amount.
- Investment Returns: The returns on investments are often expressed as percentage growth or percentage loss.
3. Business and Economics:
- Market Share: Businesses track their market share (the percentage of the total market they control) to understand their competitive position.
- Profit Margins: Profit margins, which indicate the profitability of a business, are calculated as a percentage of revenue.
- Economic Growth: Economic indicators like GDP growth are typically reported as percentage changes over time.
- Inflation Rates: Inflation rates, which measure the increase in the price level of goods and services, are expressed as percentages.
4. Science and Statistics:
- Data Analysis: Percentages are used extensively in data analysis to represent proportions and relationships within datasets.
- Probability: Probability, the chance of an event occurring, is often expressed as a percentage.
Beyond the Basics: More Complex Percentage Calculations
While calculating 10 out of 60 as a percentage is a straightforward process, more complex scenarios involving percentages might require additional steps.
1. Percentage Increase and Decrease:
Calculating percentage increases and decreases involves determining the difference between two values and expressing it as a percentage of the original value. For example, if a price increases from $100 to $120, the percentage increase is 20% (($120 - $100) / $100 × 100).
2. Calculating Original Value:
Sometimes, you might know the percentage and the final value and need to determine the original value. For instance, if a product is on sale for $80, representing a 20% discount, the original price can be calculated by reversing the percentage calculation.
3. Compound Interest:
Compound interest involves calculating interest on both the principal amount and accumulated interest over time. This calculation uses percentages to determine the growth of investments or the accumulation of debt over multiple periods.
4. Percentage Points vs. Percentages:
It's important to understand the difference between percentage points and percentages. A percentage point refers to an absolute change in percentage values, while a percentage refers to a relative change. For example, an increase from 10% to 15% is a 5-percentage point increase but a 50% relative increase ((15-10)/10 x 100).
Practical Examples: Applying Percentage Calculations
Let's explore a few practical scenarios demonstrating the importance of understanding percentages:
Scenario 1: Retail Discount
A clothing store offers a 30% discount on all items. If a shirt is originally priced at $50, what is the discounted price?
- Calculation: 30% of $50 = 0.30 × $50 = $15
- Discounted Price: $50 - $15 = $35
Scenario 2: Investment Return
An investment of $1,000 increases to $1,150 after one year. What is the percentage return on investment?
- Calculation: (($1,150 - $1,000) / $1,000) × 100 = 15%
Scenario 3: Test Score Analysis
A student scores 40 out of 50 on a math test and 30 out of 40 on a science test. Which test did the student perform better on, in terms of percentage?
- Math Test Percentage: (40/50) × 100 = 80%
- Science Test Percentage: (30/40) × 100 = 75%
- Conclusion: The student performed better on the math test.
Mastering Percentages: Tips and Resources
To enhance your understanding and proficiency with percentage calculations, consider these tips:
- Practice Regularly: Consistent practice is crucial to mastering any mathematical skill, including percentage calculations. Solve various problems to build your confidence and understanding.
- Utilize Online Calculators: Online percentage calculators can be valuable tools for verifying your calculations and exploring different scenarios. However, it's crucial to understand the underlying principles to solve problems independently.
- Seek Additional Resources: Numerous online tutorials, videos, and educational materials can help you deepen your understanding of percentage calculations and their applications.
Conclusion: The Ubiquity of Percentage Calculations
Percentages are an integral part of our daily lives, impacting our personal finances, academic pursuits, and professional endeavors. Understanding how to calculate and interpret percentages is a valuable skill that enhances decision-making capabilities across various domains. The seemingly simple calculation of 10 out of 60 as a percentage (16.67%) serves as a gateway to understanding the broader applications and significance of this fundamental mathematical concept. By mastering percentage calculations, you equip yourself with a powerful tool for navigating the quantitative aspects of the world around you.
Latest Posts
Latest Posts
-
Journal Of Hazardous Materials Advances Impact Factor 2023
May 27, 2025
-
Journal Of Chromatography Open Impact Factor
May 27, 2025
-
Transportation Research Part A Policy And Practice
May 27, 2025
-
Optics And Laser Technology Impact Factor
May 27, 2025
-
The American Journal Of Emergency Medicine
May 27, 2025
Related Post
Thank you for visiting our website which covers about 10 Out Of 60 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.