1 Is What Percent Of 30
listenit
May 25, 2025 · 4 min read
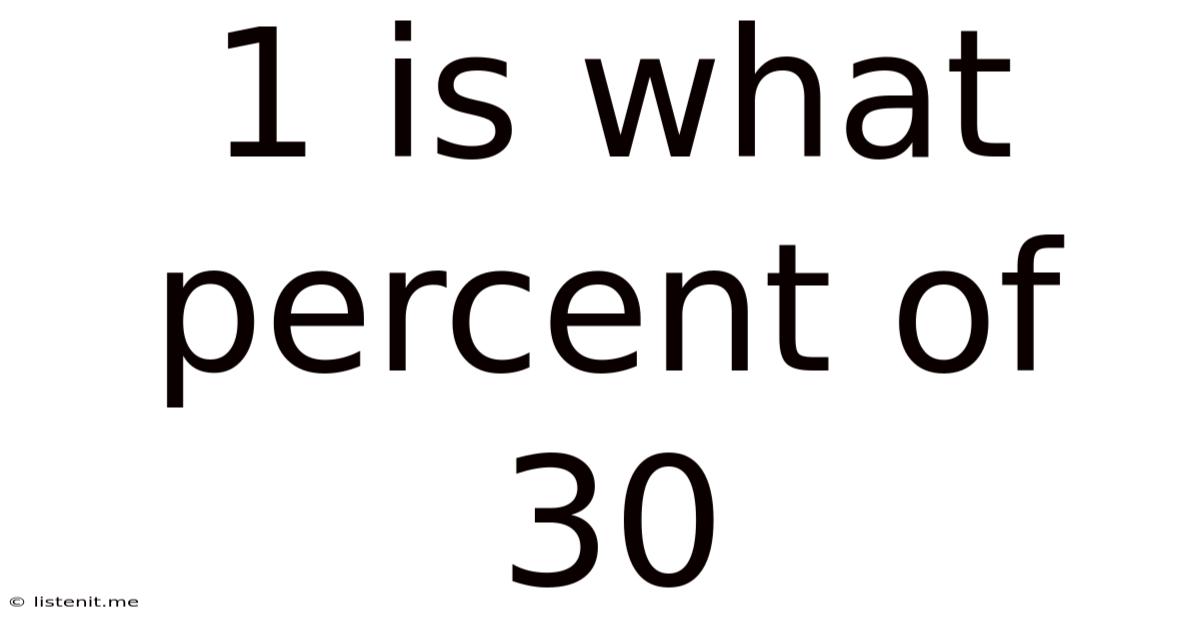
Table of Contents
1 is What Percent of 30? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill with applications spanning numerous fields, from everyday finances to complex scientific analyses. This article dives deep into the question, "1 is what percent of 30?", providing a step-by-step solution, exploring different calculation methods, and showcasing practical applications. We'll also delve into the broader concept of percentage calculations, equipping you with the knowledge to tackle similar problems with confidence.
Understanding Percentages
Before tackling our specific problem, let's establish a solid understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Calculating "1 is What Percent of 30?"
There are several ways to calculate what percentage 1 represents of 30. Let's explore the most common methods:
Method 1: Using the Formula
The fundamental formula for percentage calculations is:
(Part / Whole) * 100 = Percentage
In our case:
- Part: 1
- Whole: 30
Substituting these values into the formula:
(1 / 30) * 100 = 3.333...%
Therefore, 1 is approximately 3.33% of 30.
Method 2: Proportion Method
This method uses proportions to solve for the unknown percentage. We can set up a proportion as follows:
1/30 = x/100
Where 'x' represents the percentage we're trying to find. To solve for x, we cross-multiply:
30x = 100
x = 100 / 30
x ≈ 3.33%
This method confirms our previous calculation.
Method 3: Using Decimal Conversion
We can convert the fraction 1/30 into a decimal and then multiply by 100 to find the percentage:
1 / 30 ≈ 0.0333
0.0333 * 100 ≈ 3.33%
This approach provides an alternative, straightforward calculation.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios:
1. Finance and Budgeting:
- Interest rates: Calculating interest earned on savings accounts or interest paid on loans relies heavily on percentage calculations.
- Discounts and sales: Determining the final price of an item after a percentage discount requires calculating the discounted amount. For example, a 20% discount on a $50 item means a discount of ($50 * 0.20) = $10, resulting in a final price of $40.
- Taxes: Calculating sales tax, income tax, or property tax involves applying a percentage to the taxable amount.
- Investment returns: Tracking investment performance necessitates calculating percentage gains or losses.
2. Science and Research:
- Data analysis: Percentages are fundamental in expressing proportions and trends within data sets. For instance, scientists might report the percentage of a population exhibiting a specific characteristic.
- Experimental results: Percentages often represent success rates or error margins in scientific experiments.
- Statistical analysis: Many statistical measures, such as percentages, are used to draw meaningful conclusions from data.
3. Everyday Life:
- Tip calculation: Calculating a tip at a restaurant usually involves determining a percentage of the bill. A 15% tip on a $75 meal is ($75 * 0.15) = $11.25.
- Grade calculations: Many academic systems use percentages to represent grades. A student scoring 25 out of 30 on a test achieves (25/30) * 100 ≈ 83.33%.
- Recipe scaling: Adjusting recipe amounts often involves using percentages to increase or decrease ingredient quantities. For example, doubling a recipe involves increasing each ingredient by 100%.
Advanced Percentage Calculations
While the problem "1 is what percent of 30?" is relatively straightforward, let's explore some more complex scenarios that build on the fundamental principles we've discussed:
1. Finding the Whole when given the Part and Percentage:
If we know that 10% of a number is 5, we can calculate the whole number using the formula:
(Part / Percentage) * 100 = Whole
(5 / 10) * 100 = 50
Therefore, the whole number is 50.
2. Finding the Part when given the Whole and Percentage:
If we want to find 25% of 80, we calculate:
(Percentage / 100) * Whole = Part
(25 / 100) * 80 = 20
So, 25% of 80 is 20.
3. Percentage Change:
Calculating percentage change is used to determine the increase or decrease in a value over time. The formula is:
((New Value - Old Value) / Old Value) * 100 = Percentage Change
For example, if a stock price rises from $50 to $60, the percentage change is:
((60 - 50) / 50) * 100 = 20%
Troubleshooting Common Percentage Calculation Errors
Even simple percentage calculations can sometimes lead to errors. Here are a few common pitfalls to avoid:
- Incorrect order of operations: Always follow the order of operations (PEMDAS/BODMAS) when performing calculations involving multiplication and division.
- Using the wrong formula: Ensure you're using the appropriate formula for the specific problem you're trying to solve.
- Rounding errors: Be mindful of rounding errors, especially when dealing with decimals. Rounding too early can significantly affect the final result.
Conclusion: Mastering Percentage Calculations
Understanding percentage calculations is an invaluable skill with widespread applications. From managing personal finances to analyzing scientific data, the ability to confidently work with percentages empowers you to make informed decisions and solve various problems effectively. By mastering the different methods presented in this article, and by avoiding common errors, you can confidently tackle any percentage-related challenge that comes your way. Remember to practice regularly and apply your knowledge to real-world situations to reinforce your understanding. The seemingly simple question, "1 is what percent of 30?", serves as a powerful gateway to unlocking a world of quantitative understanding.
Latest Posts
Latest Posts
-
What Is 25 Off 75 Dollars
May 25, 2025
-
What Percent Is Equivalent To 11 20
May 25, 2025
-
What Is 75 Off Of 35
May 25, 2025
-
Greatest Common Factor Of 39 And 52
May 25, 2025
-
What Is 6 Out Of 15 As A Percentage
May 25, 2025
Related Post
Thank you for visiting our website which covers about 1 Is What Percent Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.