1 Is 1/10 Of What Number
listenit
May 11, 2025 · 4 min read
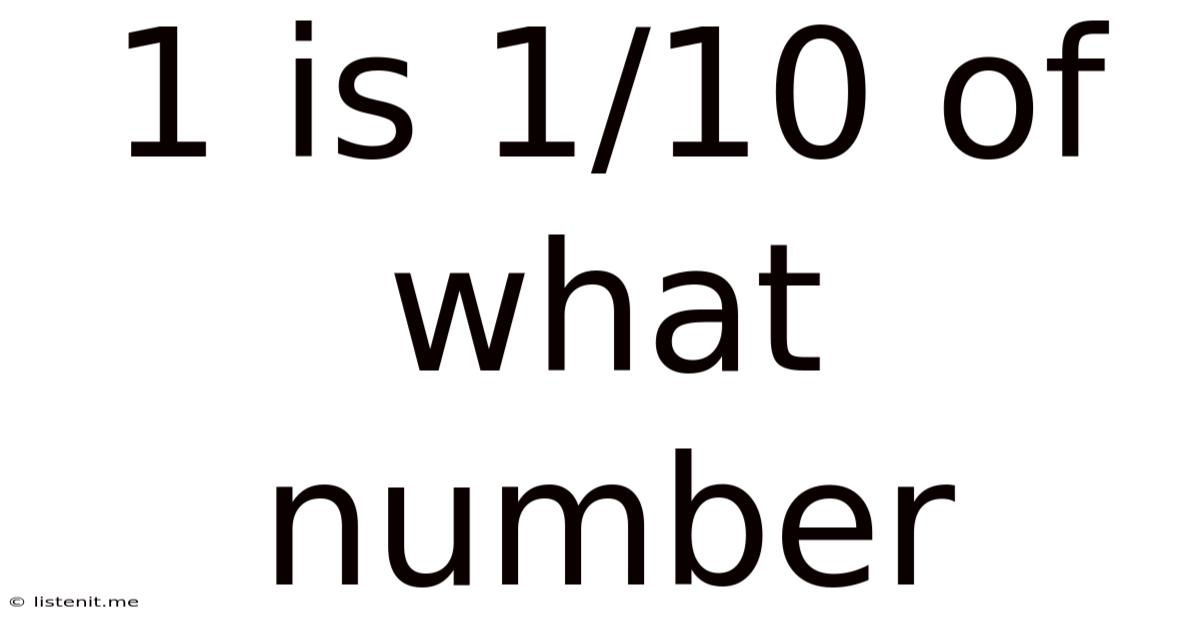
Table of Contents
1 is 1/10 of What Number? Unpacking the Fundamentals of Fractions and Algebra
This seemingly simple question, "1 is 1/10 of what number?", opens a door to a fascinating world of mathematical concepts. It's a gateway to understanding fractions, proportions, and the power of algebraic equations. While the answer might seem immediately obvious to some, delving deeper reveals the underlying principles and their broader applications. This article will thoroughly explore this question, explaining the solution step-by-step and expanding on the fundamental math involved.
Understanding the Problem: Deconstructing the Question
The question, "1 is 1/10 of what number?", presents a problem in the form of a proportion. It essentially states that 1 represents one-tenth of an unknown quantity. To solve this, we need to translate this word problem into a mathematical equation. This translation is the key to unlocking the solution.
Let's break down the key components:
- "1 is": This translates directly to "1 =". We establish 1 as the known value.
- "1/10 of": This indicates multiplication. "Of" in mathematical language often signifies multiplication. So, "1/10 of" becomes (1/10) * .
- "what number?": This represents our unknown quantity, which we'll denote with the variable 'x'.
Therefore, the complete mathematical equation becomes:
1 = (1/10) * x
Solving the Equation: Applying Algebraic Principles
Now that we have our equation, we can solve for 'x', the unknown number. Solving for 'x' involves isolating it on one side of the equation. This is achieved using the principles of algebra, specifically inverse operations.
Step 1: Eliminate the fraction:
To eliminate the fraction (1/10), we multiply both sides of the equation by its reciprocal, which is 10/1 or simply 10. This is because multiplying a fraction by its reciprocal always results in 1.
(10) * 1 = (10) * (1/10) * x
Step 2: Simplify:
This simplifies to:
10 = x
Therefore, x = 10
Verifying the Solution: Checking Your Work
It's always a good practice to check your solution to ensure accuracy. Let's substitute x = 10 back into the original equation:
1 = (1/10) * 10
1 = 1
The equation holds true, confirming that our solution, x = 10, is correct. 1 is indeed 1/10 of 10.
Expanding the Concept: Proportions and Ratios
The problem we just solved is a classic example of a proportion. A proportion is a statement that two ratios are equal. A ratio is a comparison of two quantities. In our problem, the ratio 1:x is equal to the ratio 1:10.
This concept of proportions extends far beyond simple number problems. It's used extensively in various fields including:
- Scaling: Enlarging or reducing images, maps, or blueprints.
- Mixing: Determining the correct ratios of ingredients in recipes or chemical solutions.
- Finance: Calculating interest rates, loan repayments, and investment returns.
- Science: Analyzing experimental data and establishing relationships between variables.
Beyond the Basics: More Complex Proportions
Let's explore more complex variations of this problem to solidify our understanding. What if the problem were:
"5 is 1/10 of what number?"
Following the same steps:
- Translate into an equation: 5 = (1/10) * x
- Multiply both sides by 10: 50 = x
- Verify: 5 = (1/10) * 50 (True)
The answer is 50. Notice that by increasing the initial value (from 1 to 5), the resulting unknown number also increases proportionally.
What about a problem like:
"1 is 2/5 of what number?"
- Equation: 1 = (2/5) * x
- Multiply both sides by 5/2 (the reciprocal of 2/5): (5/2) * 1 = (5/2) * (2/5) * x
- Simplify: 5/2 = x
- Verify: 1 = (2/5) * (5/2) (True)
The answer is 5/2 or 2.5. This demonstrates the application of the same principles to fractions.
Applications in Real-World Scenarios
The ability to solve such proportional problems is invaluable in everyday life. Consider these examples:
- Shopping: If a shirt is on sale for 10% off, and the discount is $5, what was the original price? (This is equivalent to the problem we initially solved).
- Cooking: If a recipe calls for 1/4 cup of sugar, and you want to double the recipe, how much sugar do you need?
- Travel: If you've driven 1/3 of a 300-mile journey, how many miles have you covered?
Developing Mathematical Fluency
Mastering the ability to solve problems like "1 is 1/10 of what number?" is a crucial step in developing mathematical fluency. It reinforces the fundamental principles of algebra, fractions, and proportions—concepts that form the backbone of many more advanced mathematical topics. The more you practice solving these types of problems, the more confident and proficient you'll become in tackling complex mathematical challenges.
Conclusion: The Power of Proportional Reasoning
This seemingly simple question, "1 is 1/10 of what number?", has unveiled a wealth of mathematical concepts. By understanding the underlying principles of fractions, proportions, and algebra, we've not only solved the problem but have also explored its broader applications and significance in various aspects of life. The key takeaway is the power of proportional reasoning—a vital skill applicable far beyond the confines of the classroom. Continue practicing these concepts and watch your mathematical abilities flourish!
Latest Posts
Latest Posts
-
Why Do Electric Field Lines Never Cross
May 13, 2025
-
1 10 As A Percent And Decimal
May 13, 2025
-
Can All Minerals Be A Gemstone
May 13, 2025
-
Multicellular Heterotrophs Without A Cell Wall
May 13, 2025
-
What Are The Gcf Of 48
May 13, 2025
Related Post
Thank you for visiting our website which covers about 1 Is 1/10 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.