1/8 Divided By 3/4 In Fraction Form
listenit
May 23, 2025 · 4 min read
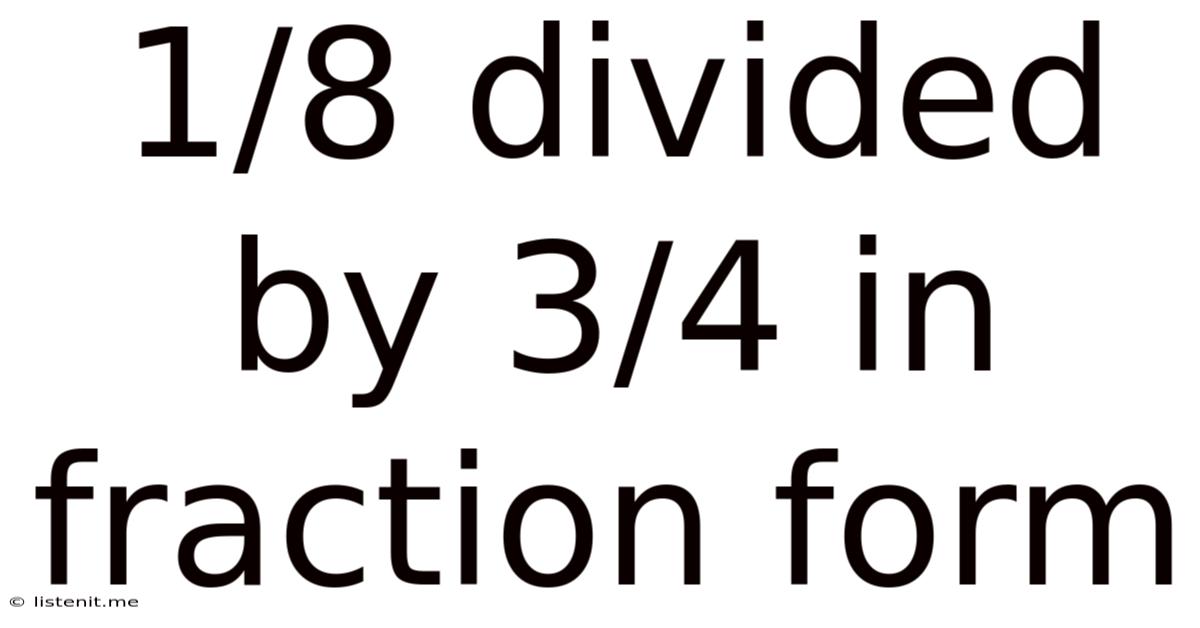
Table of Contents
1/8 Divided by 3/4 in Fraction Form: A Comprehensive Guide
Dividing fractions can seem daunting, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through dividing 1/8 by 3/4, explaining the steps involved, providing alternative methods, and exploring the underlying mathematical principles. We'll also delve into practical applications and offer tips for mastering fraction division.
Understanding Fraction Division
Before we tackle the specific problem of 1/8 divided by 3/4, let's review the fundamental concept of dividing fractions. The key is to remember that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 3/4 is 4/3.
This principle allows us to convert a division problem into a multiplication problem, which is generally easier to solve. The formula is:
a/b ÷ c/d = a/b × d/c
Where 'a', 'b', 'c', and 'd' represent numbers.
Solving 1/8 Divided by 3/4
Now, let's apply this principle to our problem: 1/8 divided by 3/4.
-
Find the reciprocal of the second fraction: The reciprocal of 3/4 is 4/3.
-
Change the division to multiplication: Our problem now becomes: 1/8 × 4/3
-
Multiply the numerators: 1 × 4 = 4
-
Multiply the denominators: 8 × 3 = 24
-
Simplify the resulting fraction: The resulting fraction is 4/24. We can simplify this by dividing both the numerator and the denominator by their greatest common divisor, which is 4.
4 ÷ 4 = 1 24 ÷ 4 = 6
Therefore, the simplified answer is 1/6.
So, 1/8 divided by 3/4 equals 1/6.
Alternative Methods and Visual Representations
While the reciprocal method is the most common and efficient approach, other methods can help solidify your understanding.
Method 2: Using Common Denominators
This method involves finding a common denominator for both fractions and then dividing the numerators.
-
Find a common denominator: The least common multiple of 8 and 4 is 8.
-
Rewrite the fractions with the common denominator: 1/8 remains as 1/8, and 3/4 becomes 6/8 (multiplying the numerator and denominator of 3/4 by 2).
-
Divide the numerators: 1 ÷ 6 = 1/6
This method might seem more complex in this instance, but it's useful when dealing with more complicated fractions.
Visual Representation
Imagine you have a pizza cut into 8 slices. You have 1 slice (1/8). If you want to divide this slice into portions representing 3/4, you're essentially asking how many (3/4)-sized portions fit into your single slice. The answer is 1/6, meaning your single slice is 1/6 of a (3/4)-sized portion. This visual approach provides an intuitive understanding of the result.
Practical Applications of Fraction Division
Fraction division isn't just an abstract mathematical concept; it has numerous real-world applications. Consider these examples:
-
Baking: If a recipe calls for 3/4 cup of flour and you only want to make 1/8 of the recipe, you'll need to divide 3/4 by 8 to determine the amount of flour needed.
-
Sewing: Dividing fabric lengths to create multiple smaller pieces requires fraction division.
-
Construction: Calculating the amount of material needed for a project often involves dividing fractions.
-
Cooking: Adjusting recipe quantities based on the number of servings requires dividing fractions.
Mastering Fraction Division: Tips and Tricks
Here are some tips to help you master fraction division:
-
Practice Regularly: Consistent practice is crucial for developing fluency with fraction division. Solve various problems, starting with simple ones and gradually increasing the complexity.
-
Understand the Concept: Focus on grasping the core principle of dividing by the reciprocal. This understanding will help you tackle more challenging problems.
-
Simplify Fractions: Always simplify your fractions to their lowest terms. This makes the calculations easier and presents the answer in its most concise form.
-
Use Visual Aids: Visual aids, like diagrams or real-world objects, can help you understand the concept of fraction division intuitively.
-
Check Your Work: Always double-check your calculations to ensure accuracy. You can verify your answer by multiplying the quotient by the divisor; the result should be the dividend.
Expanding Your Knowledge: Beyond Basic Fraction Division
While this article focused on dividing simple fractions, the principles extend to more complex scenarios:
-
Dividing mixed numbers: Convert mixed numbers into improper fractions before applying the reciprocal method.
-
Dividing fractions with variables: The same rules apply; treat variables as you would numbers.
-
Dividing decimals: Convert decimals to fractions before performing the division.
Conclusion
Dividing fractions, particularly 1/8 divided by 3/4, might seem intimidating initially, but with a clear understanding of the reciprocal method and consistent practice, it becomes a manageable skill. By understanding the underlying principles and employing various techniques, you can confidently tackle fraction division problems and apply this crucial mathematical concept to various real-world scenarios. Remember to practice regularly, utilize visual aids where necessary, and always check your work for accuracy. Mastering fraction division opens doors to a deeper understanding of mathematics and its practical applications in everyday life.
Latest Posts
Latest Posts
-
What Are The Consequences Of Having Pyrimidine Dimers In Dna
Jun 05, 2025
-
Does Pi Rads 5 Mean Aggressive Cancer
Jun 05, 2025
-
Is Hepatitis And Herpes The Same Thing
Jun 05, 2025
-
What Is A Polar Amino Acid
Jun 05, 2025
-
Spane Scale Of Emotion Research Project
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about 1/8 Divided By 3/4 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.