1 8 Divided By 1 2
listenit
May 21, 2025 · 5 min read
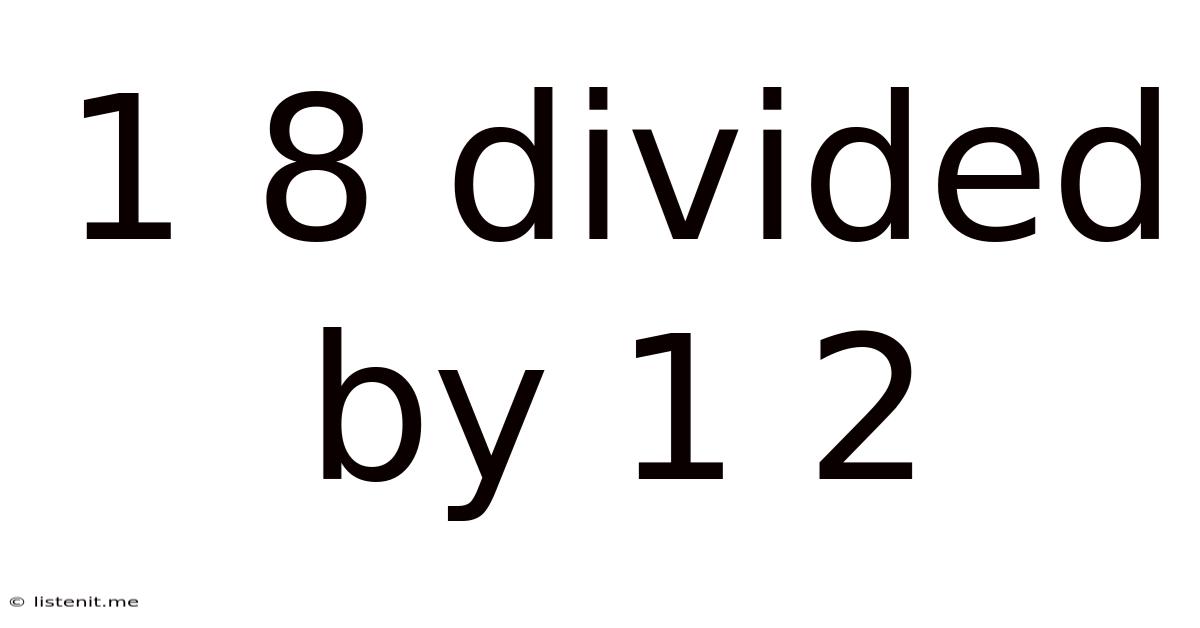
Table of Contents
1/8 Divided by 1/2: A Deep Dive into Fraction Division
Dividing fractions can seem daunting, but with a clear understanding of the process and a bit of practice, it becomes second nature. This article will explore the seemingly simple problem of 1/8 divided by 1/2, not just providing the answer, but delving deep into the underlying principles, offering multiple approaches to solving the problem, and demonstrating its relevance in real-world scenarios.
Understanding Fraction Division
Before tackling our specific problem, let's solidify the fundamental concepts of fraction division. The core idea is to understand what division means. When we divide one number by another, we're essentially asking: "How many times does the second number fit into the first?" This concept applies equally to fractions.
For example, if we divide 6 by 2, we ask: "How many times does 2 fit into 6?" The answer, of course, is 3. The same logic extends to fractions. When we divide 1/8 by 1/2, we're asking: "How many times does 1/2 fit into 1/8?" Intuitively, it's clear that 1/2 is larger than 1/8, meaning it fits into 1/8 less than once. Our answer will be a fraction less than 1.
Method 1: The "Keep, Change, Flip" Method
This is arguably the most popular and widely taught method for dividing fractions. It involves three simple steps:
- Keep: Keep the first fraction as it is.
- Change: Change the division sign to a multiplication sign.
- Flip: Flip (or find the reciprocal of) the second fraction.
Applying this to our problem:
1/8 ÷ 1/2 becomes 1/8 × 2/1
Now, we simply multiply the numerators (top numbers) and the denominators (bottom numbers):
(1 × 2) / (8 × 1) = 2/8
This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 2:
2/8 = 1/4
Therefore, 1/8 divided by 1/2 is 1/4.
Method 2: Using Common Denominators
This method provides a more visual understanding of the division process. It involves finding a common denominator for both fractions and then dividing the numerators.
First, we find a common denominator for 1/8 and 1/2. The least common multiple of 8 and 2 is 8. We rewrite the fractions with the common denominator:
1/8 remains as 1/8
1/2 becomes 4/8 (multiplying both numerator and denominator by 4)
Now, we divide the numerators:
1 ÷ 4 = 1/4
This confirms our previous result: 1/4. This method emphasizes the concept of "how many times" one fraction fits into another, more directly.
Method 3: Visual Representation
Visualizing the problem can be incredibly helpful, especially for beginners. Imagine a pizza cut into 8 slices. 1/8 represents one slice. 1/2 represents four slices. The question is: "How many times does a group of four slices (1/2) fit into one slice (1/8)?" Clearly, it doesn't fit at all, a whole group. It’s a portion of a group of four. A single slice is 1/4 of a group of four slices.
This visual representation reinforces the answer: 1/4.
Real-World Applications
While seemingly abstract, fraction division has numerous real-world applications. Consider these examples:
- Cooking: A recipe calls for 1/2 cup of flour, but you only have 1/8 cup. Dividing 1/8 by 1/2 tells you that you have 1/4 of the required flour.
- Sewing: You have 1/8 of a yard of fabric and need to cut it into pieces that are 1/2 a yard each. Fraction division helps you understand you cannot cut even one piece of the required size.
- Construction: Measuring materials for a project often involves fractions. Dividing fractional measurements is crucial for accuracy and efficiency.
- Time Management: Dividing up a portion of your day into smaller task blocks can involve fractions. If you want to allocate 1/8 of your day to a task, and one sub-task requires 1/2 that time, you can use fraction division to find the time required for that sub-task.
Extending the Concept: Dividing Fractions with Larger Numbers
The principles discussed above apply equally to more complex fraction division problems. For example, let's consider 5/6 ÷ 2/3:
Using the "Keep, Change, Flip" method:
5/6 ÷ 2/3 = 5/6 × 3/2 = (5 × 3) / (6 × 2) = 15/12
Simplifying the resulting fraction:
15/12 = 5/4 or 1 1/4
The process remains consistent: keep the first fraction, change the division to multiplication, and flip the second fraction. Always simplify the final fraction if possible.
Addressing Potential Difficulties and Common Mistakes
A common mistake in fraction division is forgetting to flip the second fraction. Students sometimes mistakenly multiply both fractions as they are, resulting in an incorrect answer. Always remember the three steps: Keep, Change, Flip.
Another potential hurdle is simplifying the resulting fraction. It's crucial to simplify fractions to their lowest terms to provide the most concise and accurate answer. Understanding greatest common divisors is crucial for efficient simplification.
Conclusion: Mastering Fraction Division
Mastering fraction division is a fundamental skill with broad applications across various fields. By understanding the underlying principles and practicing different methods, you can confidently tackle even complex fraction division problems. Remember the three main approaches covered: the "Keep, Change, Flip" method, the common denominator method, and the visual representation. Each method offers a unique approach, helping solidify your understanding and making fraction division a less daunting task. Regular practice is key to building confidence and accuracy in performing fraction divisions. This comprehensive guide provides you with the tools and knowledge necessary to tackle all your fraction division challenges with ease and efficiency. The seemingly simple problem of 1/8 divided by 1/2 serves as a perfect gateway to mastering the art of fraction division and expanding your mathematical prowess.
Latest Posts
Latest Posts
-
Is Hepatitis And Herpes The Same Thing
Jun 05, 2025
-
What Is A Polar Amino Acid
Jun 05, 2025
-
Spane Scale Of Emotion Research Project
Jun 05, 2025
-
Definition Of Channel Protein In Biology
Jun 05, 2025
-
Castor Oil And The Lymphatic System
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about 1 8 Divided By 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.