1/6 Divided By 6 Divided By 6
listenit
May 25, 2025 · 5 min read
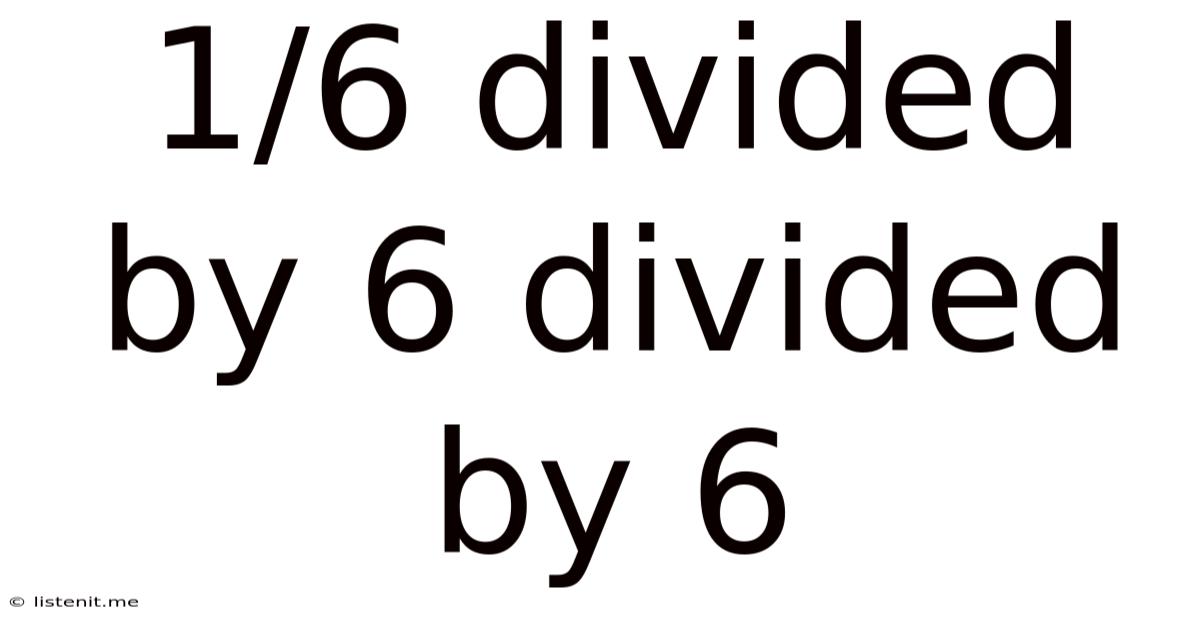
Table of Contents
Decoding 1/6 Divided by 6 Divided by 6: A Deep Dive into Fraction Division
The seemingly simple mathematical expression "1/6 divided by 6 divided by 6" can be surprisingly complex when we delve into the underlying principles of fraction division and the order of operations. This article will not only solve this specific problem but also equip you with the knowledge to tackle similar fractional division challenges. We'll explore various approaches, highlighting the importance of understanding the order of operations (often remembered by the acronym PEMDAS/BODMAS) and the mechanics of dividing fractions. We'll also touch upon the practical applications of such calculations in various fields.
Understanding the Order of Operations (PEMDAS/BODMAS)
Before jumping into the calculation, let's refresh our understanding of the order of operations. PEMDAS/BODMAS dictates the sequence in which we should perform mathematical operations:
- Parentheses/Brackets: Solve expressions within parentheses or brackets first.
- Exponents/Orders: Evaluate exponents or powers next.
- Multiplication and Division: Perform multiplication and division from left to right. They have equal precedence.
- Addition and Subtraction: Perform addition and subtraction from left to right. They also have equal precedence.
In our problem, "1/6 divided by 6 divided by 6," we only have division operations. Therefore, we proceed from left to right.
Method 1: Step-by-Step Division
Let's solve the problem step-by-step, adhering strictly to the order of operations:
Step 1: (1/6) ÷ 6
To divide a fraction by a whole number, we can rewrite the whole number as a fraction (6/1) and then multiply the first fraction by the reciprocal of the second fraction. The reciprocal of a fraction is simply the fraction flipped upside down.
(1/6) ÷ 6 = (1/6) ÷ (6/1) = (1/6) × (1/6) = 1/36
Step 2: (1/36) ÷ 6
Now, we repeat the process with the result from Step 1:
(1/36) ÷ 6 = (1/36) ÷ (6/1) = (1/36) × (1/6) = 1/216
Therefore, the solution to "1/6 divided by 6 divided by 6" is 1/216.
Method 2: Combining the Divisions
Alternatively, we can combine the divisions into a single expression:
(1/6) ÷ 6 ÷ 6 = (1/6) ÷ (6 × 6) = (1/6) ÷ 36
Now, we proceed as in Step 2 of Method 1:
(1/6) ÷ 36 = (1/6) × (1/36) = 1/216
This method yields the same result, confirming the accuracy of our calculations. This demonstrates that grouping the divisions does not change the outcome as long as we correctly apply the order of operations.
Visualizing the Problem
It can be helpful to visualize fractional division. Imagine you have 1/6 of a pizza. You want to divide this 1/6 slice into 6 equal pieces. Then you divide each of these pieces into 6 equal parts. The final result would be a very small fraction of the original pizza - 1/216.
Practical Applications of Fractional Division
While this specific problem might seem abstract, fractional division is fundamental in many real-world scenarios:
-
Cooking and Baking: Scaling recipes up or down requires precise fractional division. If a recipe calls for 1/6 cup of flour, and you want to make only 1/6 of the recipe, you'll need to calculate 1/6 ÷ 6 to determine the required amount of flour.
-
Engineering and Construction: Precise measurements are crucial in engineering and construction. Dividing materials or lengths into fractions is a common task, often requiring multiple divisions to arrive at the final dimensions.
-
Finance: Calculating portions of investments, interest rates, or profits frequently involves fractional division.
-
Science: In scientific experiments, dividing samples or quantities often necessitates the use of fractions and their division.
-
Data Analysis: When dealing with datasets and percentages, fractional division plays a key role in extracting meaningful insights.
Expanding on Fraction Division Techniques
Let's explore some further aspects of dividing fractions, which will solidify your understanding and enhance your ability to tackle more complex problems:
Dividing Fractions by Fractions
When dividing a fraction by another fraction, the process remains similar: we multiply the first fraction by the reciprocal of the second fraction.
For example, (1/2) ÷ (1/4) = (1/2) × (4/1) = 4/2 = 2
Dividing Mixed Numbers
Mixed numbers, which combine a whole number and a fraction (e.g., 2 1/2), require an extra step before dividing. First, convert the mixed number into an improper fraction. An improper fraction has a numerator larger than its denominator.
For example, to divide 2 1/2 by 1/4, first convert 2 1/2 to an improper fraction: (2 × 2 + 1)/2 = 5/2
Then, proceed with the division as before: (5/2) ÷ (1/4) = (5/2) × (4/1) = 20/2 = 10
Decimal Equivalents
Sometimes, it can be easier to convert fractions to decimals before performing the division. For our original problem, we could have converted 1/6 to its decimal equivalent (approximately 0.1667) and then performed the divisions:
0.1667 ÷ 6 ÷ 6 ≈ 0.0046
This decimal approximation is close to the exact fraction 1/216 (approximately 0.0046). Remember that using decimal approximations might introduce slight inaccuracies, especially when dealing with repeating decimals.
Conclusion: Mastering Fractional Division
The seemingly simple expression "1/6 divided by 6 divided by 6" offers a valuable lesson in the importance of understanding the order of operations and the mechanics of fractional division. Through step-by-step calculations and visualization, we arrived at the solution: 1/216. By mastering these techniques, you're well-equipped to confidently tackle more complex fractional division problems, expanding your mathematical proficiency and ability to solve problems across various fields. Remember to always check your work and consider using multiple methods to ensure accuracy. The ability to manipulate fractions is a powerful tool in numerous academic and real-world situations. Practice regularly, and you'll soon find these calculations become second nature.
Latest Posts
Latest Posts
-
12 Out Of 24 As A Percentage
May 25, 2025
-
Find The Greatest Common Factor Of 15 And 42
May 25, 2025
-
What Is The Gcf Of 3 And 12
May 25, 2025
-
8 Out Of 14 Is What Percent
May 25, 2025
-
1979 To 2023 How Many Years
May 25, 2025
Related Post
Thank you for visiting our website which covers about 1/6 Divided By 6 Divided By 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.