1/6 Divided By 4 As A Fraction
listenit
May 24, 2025 · 5 min read
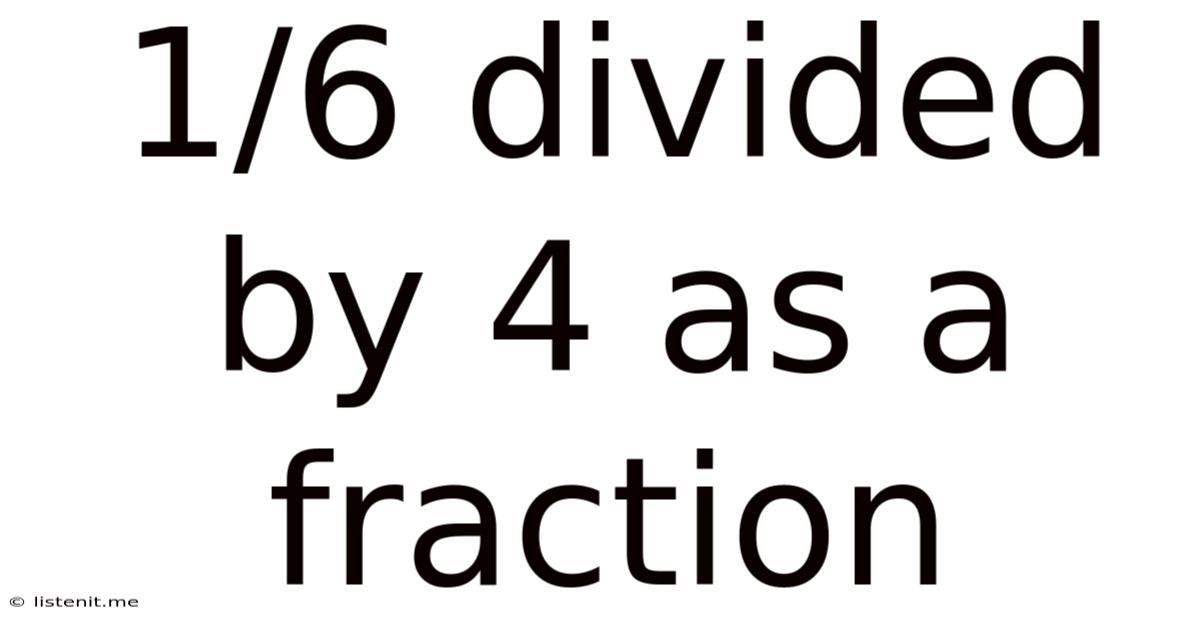
Table of Contents
1/6 Divided by 4: A Comprehensive Guide to Fraction Division
Understanding fraction division can be a stumbling block for many, but mastering it unlocks a world of mathematical possibilities. This comprehensive guide will walk you through the process of dividing 1/6 by 4, explaining the underlying concepts and providing multiple approaches to solve this problem. We’ll also explore related concepts and delve into practical applications to solidify your understanding.
Understanding Fraction Division
Before diving into the specific problem of 1/6 divided by 4, let's establish a solid foundation in fraction division. The core concept revolves around the idea of reciprocals and multiplication. Instead of directly dividing by a fraction, we multiply by its reciprocal.
The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2. The reciprocal of a whole number can be expressed as a fraction with 1 as the numerator. For instance, the reciprocal of 4 is 1/4.
The rule for dividing fractions is: Keep the first fraction the same, change the division sign to a multiplication sign, and flip the second fraction (take its reciprocal).
Solving 1/6 Divided by 4
Now, let's tackle the specific problem: 1/6 ÷ 4. Following the rule above:
- Keep the first fraction: 1/6 remains as 1/6.
- Change the division sign to multiplication: The division symbol (÷) becomes a multiplication symbol (×).
- Flip the second fraction: The reciprocal of 4 (which can be written as 4/1) is 1/4.
Therefore, the problem becomes: (1/6) × (1/4).
Multiplying Fractions
Multiplying fractions is straightforward: Multiply the numerators together and multiply the denominators together.
(1/6) × (1/4) = (1 × 1) / (6 × 4) = 1/24
Therefore, 1/6 divided by 4 is equal to 1/24.
Alternative Approaches to Fraction Division
While the reciprocal method is the most common and efficient way to divide fractions, let's explore a few alternative approaches to further solidify our understanding.
Using Visual Models
Visual representations can be helpful, especially for beginners. Imagine a pizza cut into six slices. 1/6 represents one slice. Dividing this single slice among four people means each person gets a smaller portion. To determine the size of each portion, we can divide the single slice into four equal parts. This results in 1/24 of the original pizza for each person.
Using Decimal Conversion
Another approach involves converting the fraction to a decimal and then performing the division.
1/6 ≈ 0.1667
Dividing this decimal by 4:
0.1667 ÷ 4 ≈ 0.04167
Converting this back to a fraction is more challenging and may result in an approximate value, unlike the exact fraction 1/24 obtained using the reciprocal method. This method is less precise and less efficient for this particular problem.
Expanding on Fraction Concepts: Key Related Terms and Techniques
Understanding 1/6 divided by 4 necessitates a broader understanding of fraction-related concepts. Let's explore some of these:
Proper Fractions, Improper Fractions, and Mixed Numbers:
- Proper Fraction: A fraction where the numerator is smaller than the denominator (e.g., 1/6).
- Improper Fraction: A fraction where the numerator is larger than or equal to the denominator (e.g., 7/6).
- Mixed Number: A combination of a whole number and a proper fraction (e.g., 1 1/6). It represents a whole number plus a fractional part. Improper fractions can be converted to mixed numbers and vice-versa.
Simplifying Fractions:
Simplifying, or reducing, a fraction means finding an equivalent fraction with a smaller numerator and denominator. This is done by dividing both the numerator and the denominator by their greatest common divisor (GCD). For example, 2/4 simplifies to 1/2 because the GCD of 2 and 4 is 2. In our case, 1/24 is already in its simplest form.
Finding the Least Common Denominator (LCD):
The LCD is crucial when adding or subtracting fractions with different denominators. It's the smallest multiple that both denominators share. For instance, the LCD of 1/3 and 1/6 is 6.
Converting Between Fractions, Decimals, and Percentages:
Fractions, decimals, and percentages are interconnected. Understanding how to convert between them is essential for various applications. For instance, 1/24 can be converted to a decimal (approximately 0.0417) or a percentage (approximately 4.17%).
Practical Applications of Fraction Division
Fraction division isn't just an abstract mathematical concept; it's vital for everyday life and various professions. Here are a few examples:
- Cooking: Dividing recipes to accommodate a smaller number of servings often involves fraction division.
- Sewing: Calculating fabric requirements or adjusting patterns frequently uses fractions.
- Construction: Precise measurements in construction projects often involve fractions and their division.
- Engineering: Numerous engineering calculations rely on precise fractional computations.
- Finance: Dividing shares of stocks or calculating interest rates involves fraction division.
Troubleshooting Common Mistakes in Fraction Division
Several common errors can occur when dividing fractions. Here are some points to watch out for:
- Forgetting to take the reciprocal: Remember to flip the second fraction before multiplying.
- Incorrect multiplication of numerators and denominators: Ensure careful multiplication of both the numerators and the denominators.
- Not simplifying the final answer: Always simplify the resulting fraction to its lowest terms.
Conclusion: Mastering Fraction Division
Dividing fractions, specifically as demonstrated with 1/6 divided by 4, is a fundamental skill in mathematics with far-reaching applications. Understanding the concept of reciprocals and the steps involved in fraction division will empower you to confidently tackle a wide array of mathematical problems and real-world situations. By practicing and reinforcing these concepts, you can build a strong foundation in mathematics, opening up opportunities for further exploration and understanding of more complex mathematical concepts. Remember to practice regularly to solidify your understanding and overcome any initial challenges you might face. The more you practice, the more comfortable and proficient you'll become with fraction division.
Latest Posts
Latest Posts
-
How Much Is 55000 A Year
May 24, 2025
-
3 4 To The Power Of 4
May 24, 2025
-
11 Out Of 40 Is What Percent
May 24, 2025
-
An Annuity Has Accumulated The Cash Value Of 70000
May 24, 2025
-
What Is The Gcf Of 25 And 60
May 24, 2025
Related Post
Thank you for visiting our website which covers about 1/6 Divided By 4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.