1/6 Divided By 3 In A Fraction
listenit
May 12, 2025 · 5 min read
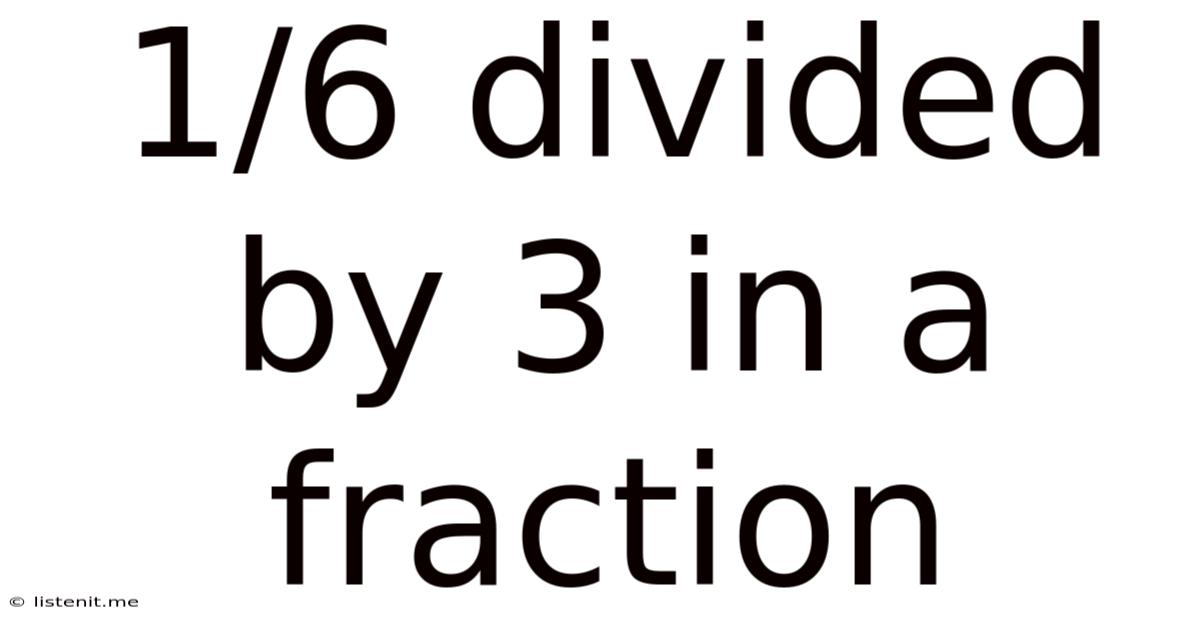
Table of Contents
1/6 Divided by 3: A Deep Dive into Fraction Division
Dividing fractions can seem daunting, but with a clear understanding of the principles involved, it becomes a straightforward process. This article will thoroughly explore the division of the fraction 1/6 by the whole number 3, explaining the steps, the underlying concepts, and providing various approaches to solve similar problems. We'll also delve into the broader context of fraction division, equipping you with the skills to tackle more complex problems confidently.
Understanding Fraction Division: The Basics
Before we tackle 1/6 divided by 3, let's establish a solid foundation in fraction division. The core concept revolves around the idea of reciprocals and multiplication. Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction inverted; the numerator becomes the denominator, and the denominator becomes the numerator. For example, the reciprocal of 2/3 is 3/2.
This principle simplifies fraction division significantly. Instead of directly dividing, we convert the division problem into a multiplication problem, making the calculations much easier. This is a fundamental rule that applies to all fraction division problems.
Solving 1/6 Divided by 3
Now, let's apply this knowledge to our specific problem: 1/6 divided by 3.
First, we need to represent the whole number 3 as a fraction. Any whole number can be expressed as a fraction with a denominator of 1. Therefore, 3 can be written as 3/1.
Our problem now becomes: (1/6) ÷ (3/1)
Next, we apply the rule of reciprocals. We change the division operation to multiplication and replace the divisor (3/1) with its reciprocal (1/3):
(1/6) x (1/3)
Now, we simply multiply the numerators together and the denominators together:
(1 x 1) / (6 x 3) = 1/18
Therefore, 1/6 divided by 3 equals 1/18.
Alternative Methods and Visual Representations
While the reciprocal method is efficient, understanding the problem conceptually can enhance your grasp of fraction division. Let's explore alternative approaches.
The "Keep, Change, Flip" Method
This mnemonic device is extremely helpful for remembering the steps involved in dividing fractions:
- Keep: Keep the first fraction (1/6) as it is.
- Change: Change the division sign (÷) to a multiplication sign (x).
- Flip: Flip the second fraction (3/1) to its reciprocal (1/3).
This method leads to the same calculation: (1/6) x (1/3) = 1/18. The "Keep, Change, Flip" method is particularly useful for students learning to divide fractions.
Visual Representation with Fraction Bars
Imagine a rectangular bar representing one whole unit. If we divide this bar into six equal parts, each part represents 1/6. Our problem asks us to divide this 1/6 piece into three equal parts. Visualizing this, it becomes clear that each of the resulting three parts would be much smaller than the original 1/6 piece. In fact, each part would represent 1/18 of the original whole bar.
This visual approach helps solidify the understanding of why the answer is 1/18. It demonstrates the reduction in size when dividing a fraction by a whole number.
Expanding the Concept: More Complex Fraction Division
Now that we’ve mastered 1/6 divided by 3, let's expand our knowledge to encompass more complex scenarios. The same principles apply, even when dealing with more intricate fractions.
Example 1: (2/5) ÷ (4/7)
- Keep, Change, Flip: (2/5) x (7/4)
- Multiply Numerators and Denominators: (2 x 7) / (5 x 4) = 14/20
- Simplify the Fraction: 14/20 simplifies to 7/10.
Therefore, (2/5) ÷ (4/7) = 7/10.
Example 2: (3/8) ÷ 2
- Express 2 as a fraction: 2/1
- Keep, Change, Flip: (3/8) x (1/2)
- Multiply: (3 x 1) / (8 x 2) = 3/16
Therefore, (3/8) ÷ 2 = 3/16.
Example 3: (5/6) ÷ (1/3)
- Keep, Change, Flip: (5/6) x (3/1)
- Multiply: (5 x 3) / (6 x 1) = 15/6
- Simplify: 15/6 simplifies to 5/2 or 2 1/2.
Therefore, (5/6) ÷ (1/3) = 5/2 or 2 1/2.
These examples highlight the consistent application of the reciprocal method. Regardless of the complexity of the fractions involved, the core principle remains the same.
Practical Applications of Fraction Division
Understanding fraction division isn't just about solving abstract mathematical problems. It has numerous practical applications in everyday life and various fields:
- Cooking and Baking: Scaling recipes up or down requires dividing or multiplying fractions accurately.
- Sewing and Crafting: Calculating fabric or material requirements often involves fraction division.
- Construction and Engineering: Precise measurements in construction projects frequently involve fractional calculations.
- Finance and Budgeting: Dividing budgets and resources effectively necessitates fractional arithmetic.
- Science and Data Analysis: Analyzing data sets and interpreting results often involves fractional computations.
Mastering fraction division equips you with the ability to handle these real-world situations with confidence and accuracy.
Troubleshooting Common Mistakes
While fraction division is relatively straightforward, certain common mistakes can lead to incorrect answers. Being aware of these pitfalls can help you avoid them:
- Forgetting to find the reciprocal: This is the most common error. Always remember to invert the second fraction (the divisor) before multiplying.
- Incorrect multiplication of numerators and denominators: Double-check your multiplication to avoid errors.
- Failing to simplify the final answer: Always simplify your fraction to its lowest terms.
Conclusion: Mastering Fraction Division for Success
Dividing fractions, particularly a problem like 1/6 divided by 3, might initially appear intimidating. However, by understanding the fundamental principle of reciprocals and applying the "Keep, Change, Flip" method, the process becomes remarkably straightforward. Through consistent practice and a grasp of the underlying concepts, you can build confidence and proficiency in tackling a wide range of fraction division problems. This skill is not just a valuable tool in mathematics but also a practical asset in various aspects of life. Remember to practice regularly and visualize the process to solidify your understanding and achieve mastery.
Latest Posts
Latest Posts
-
20 Expressed As A Fraction Is
May 12, 2025
-
How To Find Molarity Of Diluted Solution
May 12, 2025
-
5 8 Compared To 6 4
May 12, 2025
-
8 Oz Is How Many Cc
May 12, 2025
-
Which Phase Of Mitosis Takes The Longest
May 12, 2025
Related Post
Thank you for visiting our website which covers about 1/6 Divided By 3 In A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.