1 5 Divided By 3 4
listenit
May 21, 2025 · 6 min read
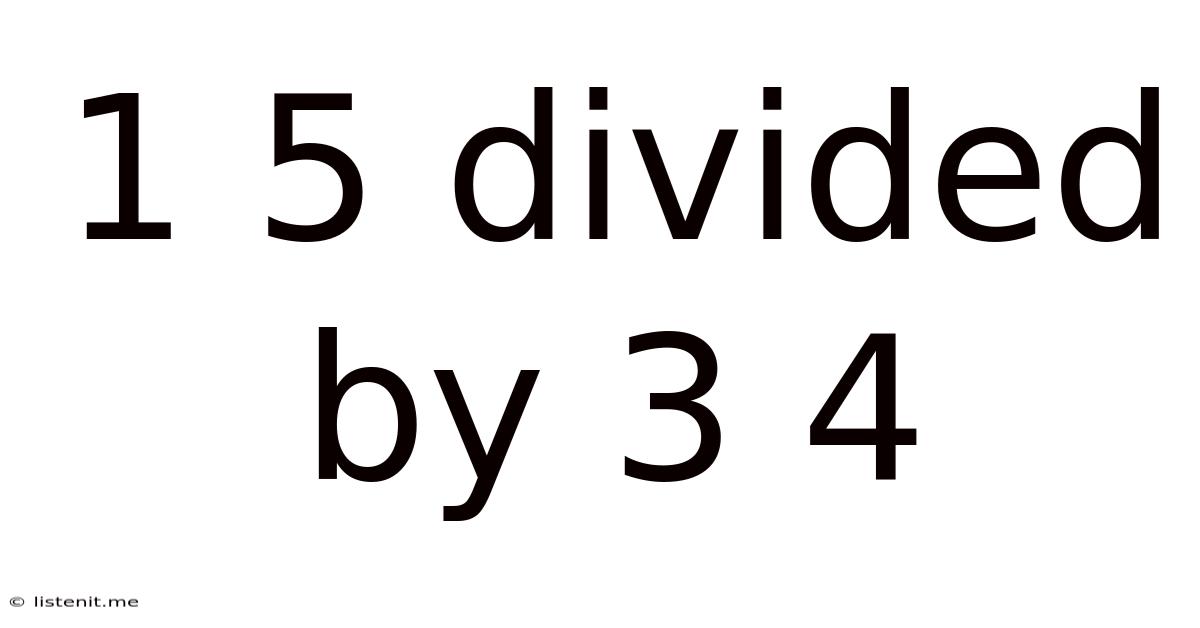
Table of Contents
1.5 Divided by 3.4: A Deep Dive into Decimal Division
The seemingly simple calculation of 1.5 divided by 3.4 might appear straightforward at first glance. However, a closer examination reveals a wealth of mathematical concepts and practical applications that extend far beyond the immediate answer. This article delves into the intricacies of this division problem, exploring various methods of calculation, its relevance in different fields, and the underlying mathematical principles involved.
Understanding Decimal Division
Before tackling 1.5 divided by 3.4 specifically, let's establish a firm understanding of decimal division. Decimal division involves dividing a number containing a decimal point (a decimal number) by another number, which may or may not also be a decimal. The process is similar to whole number division, but requires careful attention to the placement of the decimal point in the quotient (the result).
Key Concepts in Decimal Division
- Decimal Point Placement: The most critical aspect of decimal division is correctly placing the decimal point in the answer. This is often the source of errors for beginners.
- Long Division Method: For more complex decimal divisions, the long division method provides a systematic approach to obtaining the quotient. This involves a step-by-step process of dividing, multiplying, subtracting, and bringing down digits.
- Estimation and Approximation: Before performing the actual calculation, estimating the answer provides a valuable check for the final result. This helps in catching gross errors.
- Remainders and Rounding: In some cases, the division might not result in a whole number. In such instances, there will be a remainder. Depending on the context, you might need to round the answer to a specific number of decimal places.
- Converting to Fractions: Often, converting decimals to fractions can simplify the division process, especially when dealing with terminating decimals.
Calculating 1.5 Divided by 3.4: Methods and Solutions
Now, let's focus on the specific problem: 1.5 ÷ 3.4. We'll explore several methods to solve this:
Method 1: Long Division
The long division method, while seemingly cumbersome, provides a clear step-by-step process:
-
Set up the division: Arrange the numbers as 3.4 | 1.5.
-
Adjust the divisor: To simplify the division, multiply both the dividend (1.5) and the divisor (3.4) by 10 to remove the decimal point from the divisor: 34 | 15.0
-
Add a decimal point and zero: Since 15 is smaller than 34, add a decimal point to the quotient and a zero to 15, making it 150.
-
Perform long division: Divide 150 by 34. 34 goes into 150 four times (34 x 4 = 136). Subtract 136 from 150, leaving a remainder of 14.
-
Add another zero: Add another zero to the remainder, making it 140.
-
Continue the process: 34 goes into 140 four times (34 x 4 = 136). Subtract 136 from 140, leaving a remainder of 4.
-
Rounding: You can continue this process to get more decimal places, but for practical purposes, we can round the result. The quotient is approximately 0.44.
Therefore, 1.5 divided by 3.4 is approximately 0.441176.
Method 2: Using a Calculator
The simplest and most efficient method is to use a calculator. Simply input 1.5 ÷ 3.4 and the calculator will provide the answer directly, typically displaying a more precise decimal value than manual calculation.
Method 3: Converting to Fractions
Converting the decimals to fractions offers an alternative approach:
-
Convert decimals to fractions: 1.5 = 3/2 and 3.4 = 17/5
-
Divide the fractions: (3/2) ÷ (17/5) = (3/2) x (5/17) = 15/34
-
Convert back to decimal: 15/34 ≈ 0.441176
This method confirms the result obtained through long division and calculator methods.
Real-World Applications of Decimal Division
The ability to perform decimal division is crucial across many fields:
Finance and Accounting
- Calculating unit costs: Determining the cost per unit of a product when the total cost and number of units are decimal values.
- Dividing profits: Distributing profits amongst partners or shareholders based on ownership percentages represented as decimals.
- Calculating interest rates: Determining interest earned or paid on loans and investments.
Engineering and Physics
- Calculating ratios and proportions: Determining relationships between different quantities represented by decimal numbers.
- Unit conversion: Converting measurements from one unit to another (e.g., converting centimeters to inches).
- Solving equations: Decimal division often arises when solving algebraic and trigonometric equations.
Science and Data Analysis
- Calculating averages: Computing the average of a dataset containing decimal values.
- Statistical analysis: Performing statistical calculations like standard deviation and variance that involve decimal division.
- Data normalization: Scaling data to a standard range using decimal division.
Everyday Life
- Sharing expenses: Dividing the cost of a meal or a shared purchase amongst friends.
- Measuring ingredients: Dividing recipes to accommodate a smaller number of servings.
- Calculating fuel efficiency: Determining the miles per gallon of a vehicle using decimal numbers.
Expanding on the Concepts: Beyond the Basic Calculation
The seemingly simple division of 1.5 by 3.4 opens doors to a richer understanding of various mathematical concepts:
Recurring Decimals and Rational Numbers
The result of 1.5 ÷ 3.4 is a recurring decimal, meaning the decimal representation does not terminate. This highlights the relationship between rational numbers (numbers that can be expressed as a fraction of two integers) and their decimal representations. While some rational numbers have terminating decimal representations, others, like our result here, have recurring decimals.
Significance of Precision and Rounding
The level of precision required in the answer depends on the context. In certain applications, rounding to a few decimal places might be sufficient. However, in others, greater accuracy might be essential, requiring the use of more decimal places or working with fractions. Understanding the impact of rounding on the final result is crucial in many fields.
Error Analysis and Numerical Methods
When dealing with more complex calculations involving decimal division, understanding error analysis and numerical methods becomes important. These techniques help in assessing the accuracy of results and managing potential sources of errors during computations.
Advanced Mathematical Applications
Decimal division forms the bedrock of more advanced mathematical concepts, including calculus, linear algebra, and numerical analysis. Its mastery is essential for pursuing further studies in these fields.
Conclusion: Mastering Decimal Division for Success
The seemingly mundane task of dividing 1.5 by 3.4 reveals a wealth of mathematical principles and practical applications. From the simple act of using a calculator to the more intricate process of long division and fraction conversion, understanding various methods strengthens one's mathematical foundation. Furthermore, recognizing the importance of decimal division in diverse fields emphasizes its relevance and practicality in our daily lives and professional pursuits. By mastering decimal division, you equip yourself with a valuable tool for tackling numerous mathematical problems and navigating various real-world scenarios. This foundational skill will serve you well in numerous academic and professional endeavors.
Latest Posts
Latest Posts
-
What Is Worse For Liver Sugar Or Alcohol
Jun 05, 2025
-
How To Regulate Period On Spironolactone
Jun 05, 2025
-
Can Thc Be Absorbed Through Skin
Jun 05, 2025
-
Compared Human Full Grown Earless Monitor Lizard
Jun 05, 2025
-
Can Dogs Get Rotavirus From Humans
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about 1 5 Divided By 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.