1 3 Divided By 3 4 As A Fraction
listenit
May 09, 2025 · 5 min read
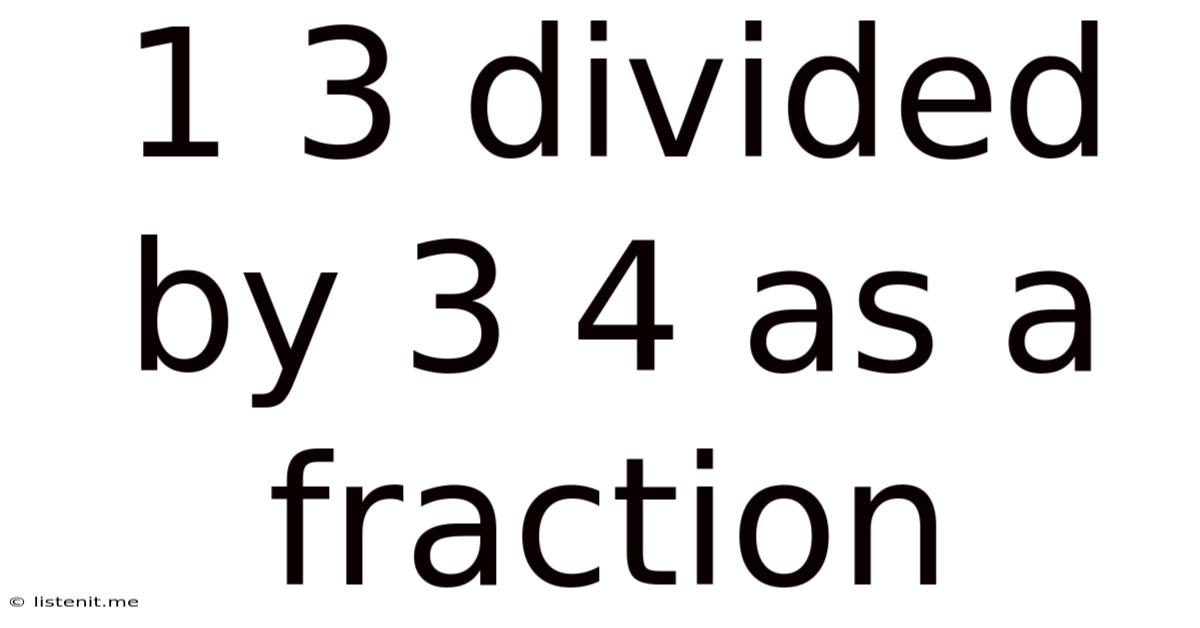
Table of Contents
1 3/4 Divided by 3/4: A Comprehensive Guide to Fraction Division
Understanding fraction division can be tricky, but mastering it unlocks a world of mathematical possibilities. This comprehensive guide will walk you through the process of dividing mixed numbers like 1 3/4 by 3/4, providing clear explanations, step-by-step instructions, and practical examples. We'll also explore the underlying concepts to solidify your understanding and build your confidence in tackling similar problems.
Understanding the Problem: 1 3/4 ÷ 3/4
Before we dive into the solution, let's break down what the problem 1 3/4 ÷ 3/4 actually means. Division, in its essence, asks the question: "How many times does one number fit into another?" In this case, we're asking: "How many times does 3/4 fit into 1 3/4?"
This problem involves a mixed number (1 3/4) and a proper fraction (3/4). To solve it effectively, we need to convert the mixed number into an improper fraction.
Converting Mixed Numbers to Improper Fractions
A mixed number combines a whole number and a fraction (e.g., 1 3/4). To convert a mixed number to an improper fraction, follow these steps:
- Multiply the whole number by the denominator: 1 x 4 = 4
- Add the numerator to the result: 4 + 3 = 7
- Keep the same denominator: The denominator remains 4.
Therefore, 1 3/4 converted to an improper fraction is 7/4.
Dividing Fractions: The Reciprocal Method
Dividing fractions is simplified using the reciprocal method. The reciprocal of a fraction is obtained by swapping its numerator and denominator. For example, the reciprocal of 3/4 is 4/3.
The process of dividing fractions involves three key steps:
- Convert any mixed numbers to improper fractions: As we did above, we transformed 1 3/4 into 7/4.
- Replace the division symbol with a multiplication symbol and use the reciprocal of the second fraction: This transforms the problem from 7/4 ÷ 3/4 to 7/4 x 4/3.
- Multiply the numerators together and the denominators together: (7 x 4) / (4 x 3) = 28/12.
Simplifying the Resulting Fraction
The result of our multiplication, 28/12, is an improper fraction. To express it as a mixed number or a simplified proper fraction, we need to simplify it:
- Find the greatest common divisor (GCD) of the numerator and the denominator: The GCD of 28 and 12 is 4.
- Divide both the numerator and the denominator by the GCD: 28 ÷ 4 = 7 and 12 ÷ 4 = 3.
This simplifies our fraction to 7/3.
Converting the Improper Fraction to a Mixed Number
While 7/3 is a perfectly acceptable answer, it's often more practical to express it as a mixed number. To do this:
- Divide the numerator by the denominator: 7 ÷ 3 = 2 with a remainder of 1.
- The quotient (2) becomes the whole number part of the mixed number: This is the number of times 3 fits into 7.
- The remainder (1) becomes the numerator of the fractional part: This is the amount left over.
- The denominator remains the same: The denominator is still 3.
Therefore, 7/3 as a mixed number is 2 1/3.
Conclusion: The Solution to 1 3/4 ÷ 3/4
By following these steps, we've definitively answered the question: 1 3/4 divided by 3/4 equals 2 1/3. This means that 3/4 fits into 1 3/4 two and one-third times.
Real-World Applications of Fraction Division
Understanding fraction division isn't just about solving textbook problems; it has numerous practical applications in everyday life and various professions. Here are a few examples:
- Cooking and Baking: Recipes often require dividing ingredients into fractions. If a recipe calls for 1 1/2 cups of flour and you want to halve the recipe, you'll need to divide 1 1/2 by 2.
- Sewing and Tailoring: Creating garments involves precise measurements, often requiring the division of fractional lengths of fabric.
- Construction and Engineering: Precise calculations involving fractions are essential in construction, from measuring materials to calculating angles.
- Finance and Budgeting: Managing finances often involves dividing budgets and expenses, sometimes expressed as fractions.
- Data Analysis and Statistics: Fraction division is frequently used in statistical calculations and data analysis.
Expanding Your Fraction Skills: Further Exploration
Mastering fraction division is a stepping stone to more advanced mathematical concepts. Here are some areas to explore further to enhance your skills:
- Complex Fractions: These involve fractions within fractions, requiring a multi-step approach to simplification.
- Fraction Multiplication and Addition/Subtraction: A solid understanding of these fundamental operations is crucial for tackling more complex fraction problems.
- Decimal Conversions: Learning to convert between fractions and decimals expands your problem-solving capabilities.
- Algebraic Expressions with Fractions: Applying fraction operations within algebraic equations is a key skill in advanced mathematics.
Practice Problems: Testing Your Knowledge
To reinforce your understanding, try solving these practice problems:
- 2 1/2 ÷ 1/4
- 3/8 ÷ 2/3
- 5 2/5 ÷ 1 1/2
- 1/3 ÷ 2 1/4
- 4 3/7 ÷ 3/14
Solving these problems will solidify your grasp of fraction division and build your confidence in tackling more challenging mathematical problems. Remember to break down each problem systematically, converting mixed numbers to improper fractions, applying the reciprocal method, and simplifying the resulting fraction. Don't be afraid to check your answers using a calculator or online fraction calculator to ensure accuracy.
Overcoming Common Mistakes in Fraction Division
Even seasoned mathematicians can make mistakes when working with fractions. Here are some common errors to avoid:
- Forgetting to convert mixed numbers: Always convert mixed numbers to improper fractions before performing any division.
- Incorrectly applying the reciprocal: Remember to use the reciprocal of the second fraction (the divisor) when converting division to multiplication.
- Errors in simplification: Carefully check your simplification steps to ensure the fraction is in its lowest terms.
- Arithmetic errors: Double-check your multiplication and division calculations to avoid simple mistakes.
By understanding these common pitfalls and practicing regularly, you can significantly improve your accuracy and confidence in fraction division. Remember, consistent practice is key to mastering any mathematical skill. Through dedicated effort and attention to detail, you can become proficient in solving fraction division problems and apply this crucial skill to various aspects of your life and studies.
Latest Posts
Latest Posts
-
How To Find Domain And Range Of Function Algebraically
May 11, 2025
-
What Is 25 Written In Its Simplest Fraction Form
May 11, 2025
-
Find The Square Root Of 361
May 11, 2025
-
Lowest Ionization Energy In Periodic Table
May 11, 2025
-
What Is The Basic Unit Of Living Things
May 11, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Divided By 3 4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.