1 3 Divided By 1 4 In Fraction Form
listenit
May 09, 2025 · 5 min read
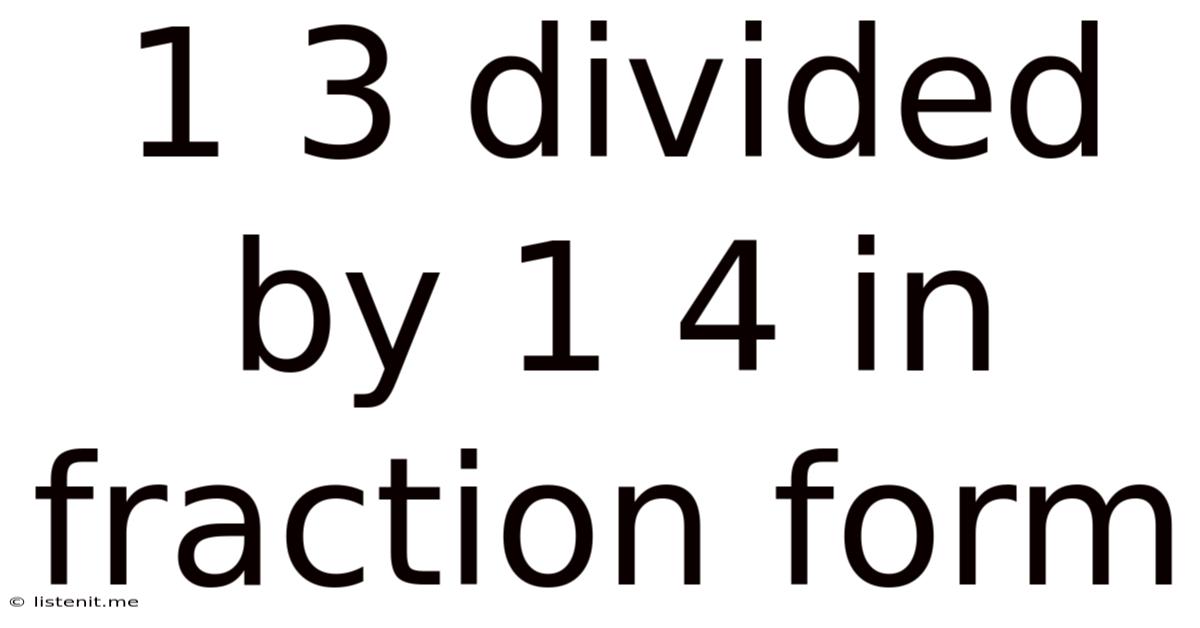
Table of Contents
1 3/4 Divided by 1 1/4 in Fraction Form: A Comprehensive Guide
This article provides a comprehensive guide on how to divide mixed numbers, specifically addressing the problem of 1 3/4 divided by 1 1/4. We will explore the process step-by-step, offering multiple approaches to solve this problem and explaining the underlying mathematical principles. We will also delve into the importance of understanding fractions and mixed numbers in various applications.
Understanding Fractions and Mixed Numbers
Before tackling the division problem, let's refresh our understanding of fractions and mixed numbers.
Fractions: A fraction represents a part of a whole. It consists of two parts: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts we have, and the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we have 3 out of 4 equal parts.
Mixed Numbers: A mixed number combines a whole number and a fraction. For example, 1 3/4 represents one whole unit and three-quarters of another unit.
Converting Mixed Numbers to Improper Fractions
Dividing mixed numbers directly can be cumbersome. The most efficient approach is to convert them into improper fractions first. An improper fraction is a fraction where the numerator is greater than or equal to the denominator.
To convert a mixed number to an improper fraction, follow these steps:
- Multiply the whole number by the denominator: In 1 3/4, multiply 1 (the whole number) by 4 (the denominator). This gives us 4.
- Add the numerator: Add the result from step 1 (4) to the numerator (3). This gives us 7.
- Keep the same denominator: The denominator remains 4.
Therefore, 1 3/4 converts to the improper fraction 7/4. Similarly, 1 1/4 converts to 5/4.
Dividing Fractions: The Reciprocal Method
Dividing fractions involves a crucial step: using the reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 3/4 is 4/3. The reciprocal of 5/4 is 4/5.
To divide fractions, we multiply the first fraction by the reciprocal of the second fraction. This can be expressed as:
(a/b) ÷ (c/d) = (a/b) x (d/c)
Solving 1 3/4 ÷ 1 1/4
Now, let's apply this to our problem: 1 3/4 ÷ 1 1/4.
- Convert to improper fractions: As shown above, 1 3/4 becomes 7/4, and 1 1/4 becomes 5/4.
- Rewrite as multiplication: The division problem becomes (7/4) ÷ (5/4). This is equivalent to (7/4) x (4/5).
- Multiply the numerators and denominators: Multiply the numerators together (7 x 4 = 28) and the denominators together (4 x 5 = 20). This gives us 28/20.
- Simplify the fraction: Both 28 and 20 are divisible by 4. Simplifying the fraction, we get 7/5.
- Convert to a mixed number (optional): To express the answer as a mixed number, divide the numerator (7) by the denominator (5). This gives us 1 with a remainder of 2. Therefore, the answer as a mixed number is 1 2/5.
Therefore, 1 3/4 ÷ 1 1/4 = 7/5 or 1 2/5
Alternative Methods and Further Exploration
While the reciprocal method is the most efficient, alternative methods exist. These include:
- Converting to decimals: Convert both mixed numbers to decimals (1 3/4 = 1.75 and 1 1/4 = 1.25) and then perform the division using a calculator. This method is less precise for certain fractions.
- Long division: Convert the mixed numbers to improper fractions and then perform long division. This is more time-consuming but demonstrates the fundamental concept of division.
Practical Applications of Fraction Division
Understanding fraction division isn't just about solving math problems; it has practical applications in many real-world scenarios:
- Cooking and Baking: Scaling recipes up or down requires dividing fractions.
- Sewing and Crafting: Calculating fabric needs or cutting materials to specific sizes often involves fraction division.
- Construction and Engineering: Precise measurements and material calculations rely heavily on understanding and manipulating fractions.
- Finance and Budgeting: Dividing resources or calculating proportions frequently necessitates fraction division.
Mastering Fractions: A Continuous Process
Mastering fractions and mixed numbers requires consistent practice and understanding of the underlying concepts. The ability to effortlessly convert between mixed numbers and improper fractions, and to utilize the reciprocal method for division, is essential for success in various mathematical applications and real-world problem-solving. By continuously practicing and applying these skills, you will build a strong foundation in mathematics and improve your ability to tackle more complex problems.
Expanding Your Knowledge: Related Concepts
To further enhance your understanding, explore related mathematical concepts such as:
- Adding and Subtracting Fractions: Mastering addition and subtraction of fractions forms the basis for understanding more complex operations.
- Multiplying Fractions: Similar to division, multiplying fractions involves a straightforward process of multiplying numerators and denominators.
- Simplifying Fractions: Learning how to simplify fractions to their lowest terms is crucial for presenting answers in their most concise form.
- Finding Common Denominators: This skill is essential for adding and subtracting fractions with different denominators.
By mastering these core concepts, you'll not only be able to confidently tackle problems like 1 3/4 divided by 1 1/4 but will also possess a strong foundation in fundamental mathematics. Remember that practice is key, so continue solving problems and exploring different approaches to solidify your understanding. The ability to work confidently with fractions is a valuable asset in numerous areas of life and study.
Latest Posts
Latest Posts
-
How Many Pounds Is 0 5 Kg
May 10, 2025
-
Which Waves Have The Highest Energy
May 10, 2025
-
How Many Square Inches In A 12 Inch Circle
May 10, 2025
-
Are Roots And X Intercepts The Same
May 10, 2025
-
Square Root Of 16 Is A Rational Number
May 10, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Divided By 1 4 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.