1 3 Divided By 1 3
listenit
May 18, 2025 · 5 min read
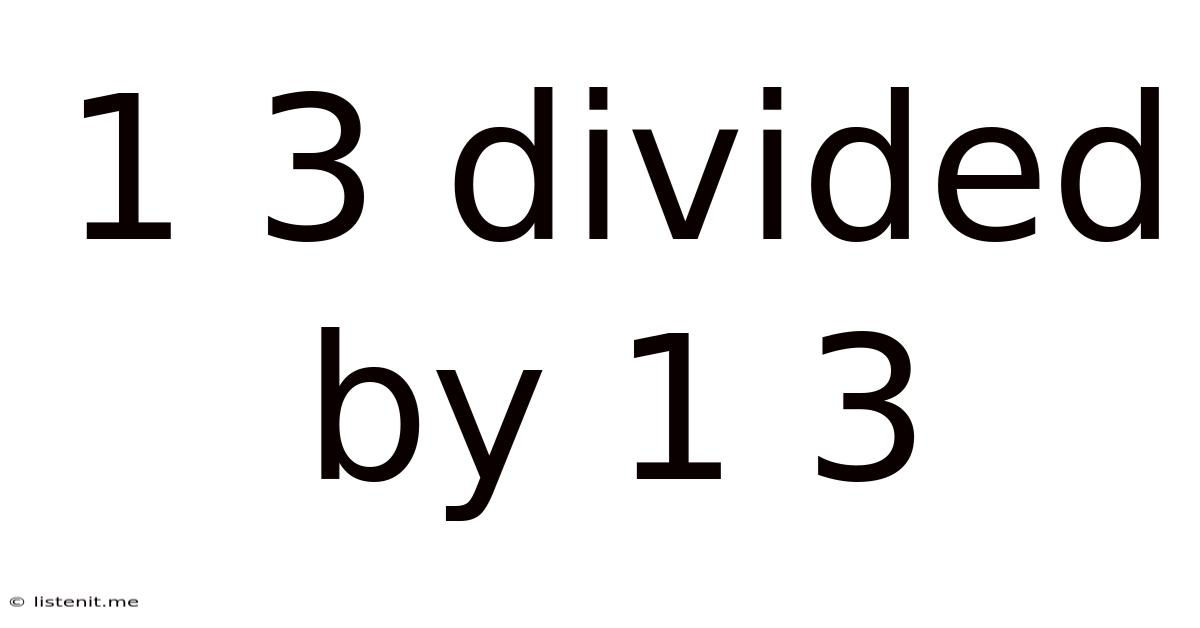
Table of Contents
1/3 Divided by 1/3: A Deep Dive into Fraction Division
Understanding fraction division can be tricky, but it's a fundamental concept in mathematics with broad applications in various fields. This comprehensive guide will explore the division of 1/3 by 1/3, explaining the process step-by-step, providing multiple approaches to solve the problem, and illustrating its relevance in real-world scenarios. We'll also delve into related concepts to solidify your understanding of fraction manipulation.
Understanding Fraction Division
Before tackling 1/3 divided by 1/3, let's refresh our understanding of fraction division in general. When we divide fractions, we're essentially asking "how many times does one fraction fit into another?" This is fundamentally different from multiplying fractions. Instead of multiplying numerators and denominators, we use a process called inverting and multiplying.
The "Keep, Change, Flip" Method: This is a popular mnemonic device to remember the steps:
- Keep: Keep the first fraction as it is.
- Change: Change the division sign to a multiplication sign.
- Flip: Flip (invert) the second fraction (reciprocal).
Then, multiply the numerators and multiply the denominators.
Solving 1/3 Divided by 1/3
Now, let's apply this knowledge to our problem: 1/3 ÷ 1/3.
Using the "Keep, Change, Flip" method:
- Keep: We keep the first fraction: 1/3
- Change: We change the division sign (÷) to a multiplication sign (×).
- Flip: We flip the second fraction (1/3) to its reciprocal, which is 3/1 (or simply 3).
This gives us: (1/3) × (3/1)
Now, we multiply the numerators and the denominators:
(1 × 3) / (3 × 1) = 3/3
Simplifying the fraction, we get: 3/3 = 1
Therefore, 1/3 divided by 1/3 equals 1.
Alternative Approaches
While the "Keep, Change, Flip" method is widely used and effective, let's explore alternative approaches to reach the same solution:
Visual Representation
Imagine you have one-third of a pizza. If you divide that one-third into portions that are also one-third in size, you'll find you only have one such portion. This visual representation confirms that 1/3 ÷ 1/3 = 1.
Using Decimal Equivalents
We can convert the fractions to decimals before performing the division. 1/3 is approximately 0.333...
Therefore, 0.333... ÷ 0.333... = 1 (approximately). Note that the slight inaccuracy is due to the repeating decimal nature of 1/3.
Conceptual Understanding
The problem essentially asks: "How many times does 1/3 fit into 1/3?" The answer is clearly one time. This approach emphasizes the intuitive understanding behind the mathematical operation.
Real-World Applications
The concept of dividing fractions, even seemingly simple ones like 1/3 ÷ 1/3, is crucial in many real-world scenarios:
-
Cooking and Baking: Dividing ingredients in recipes often involves fractions. If a recipe calls for 1/3 cup of flour, and you only want to make 1/3 of the recipe, you'll need to divide 1/3 by 3 (1/3 ÷ 3 = 1/9), determining you need 1/9 of a cup of flour.
-
Sewing and Tailoring: Cutting fabric pieces requires precise measurements, often involving fractions of inches or centimeters. Dividing fabric based on fractional patterns is a common task in this field.
-
Construction and Engineering: Precise measurements and calculations with fractions are vital for accurate construction and engineering projects. Dividing tasks into smaller, fractional parts helps with project management and resource allocation.
-
Data Analysis and Statistics: Dividing datasets and working with fractional proportions of data are essential steps in statistical analysis and data interpretation.
-
Finance and Economics: Many financial calculations involve fractions and proportions, such as determining fractional shares of ownership or calculating interest rates.
Expanding on Fraction Concepts
Let's solidify our understanding of fractions by looking at closely related concepts:
Reciprocals
The reciprocal of a number is simply 1 divided by that number. It's also known as the multiplicative inverse. For example, the reciprocal of 1/3 is 3/1 or 3. This concept is directly applied in the "Keep, Change, Flip" method for fraction division.
Equivalent Fractions
Equivalent fractions represent the same value but have different numerators and denominators. For instance, 1/3, 2/6, and 3/9 are all equivalent fractions. Understanding equivalent fractions is important for simplifying results and making comparisons.
Simplifying Fractions
Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD). For example, 3/3 simplifies to 1 because the GCD of 3 and 3 is 3.
Adding and Subtracting Fractions
To add or subtract fractions, they must have a common denominator. If they don't, you'll need to find the least common multiple (LCM) of their denominators and convert the fractions to equivalent fractions with the LCM as the denominator.
Multiplying Fractions
Multiplying fractions is straightforward: multiply the numerators and multiply the denominators. For example: (1/3) × (2/5) = 2/15
Conclusion: Mastering Fraction Division
Mastering fraction division, especially understanding simple cases like 1/3 ÷ 1/3 = 1, builds a solid foundation for more complex mathematical operations. The "Keep, Change, Flip" method provides a simple and effective approach, but understanding the underlying concepts through visual representations and real-world applications solidifies your knowledge. This thorough understanding empowers you to confidently tackle more challenging fraction problems and apply this knowledge effectively across various disciplines. Remember that practice is key to mastering these concepts. Work through various fraction division problems, using different methods to reinforce your learning. With consistent practice, you will gain fluency and confidence in your ability to handle fractions with ease.
Latest Posts
Latest Posts
-
How Much Fetal Fraction Is Needed For Gender
Jun 05, 2025
-
Florence Nightingale And Evidence Based Practice
Jun 05, 2025
-
Chances Of Getting Hit By A Tornado
Jun 05, 2025
-
Human Growth Hormone Frequency Hz Rats 1993
Jun 05, 2025
-
How To Get Rid Of Scars From Self Harm
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.