1 3 4 Divided By 2
listenit
May 18, 2025 · 6 min read
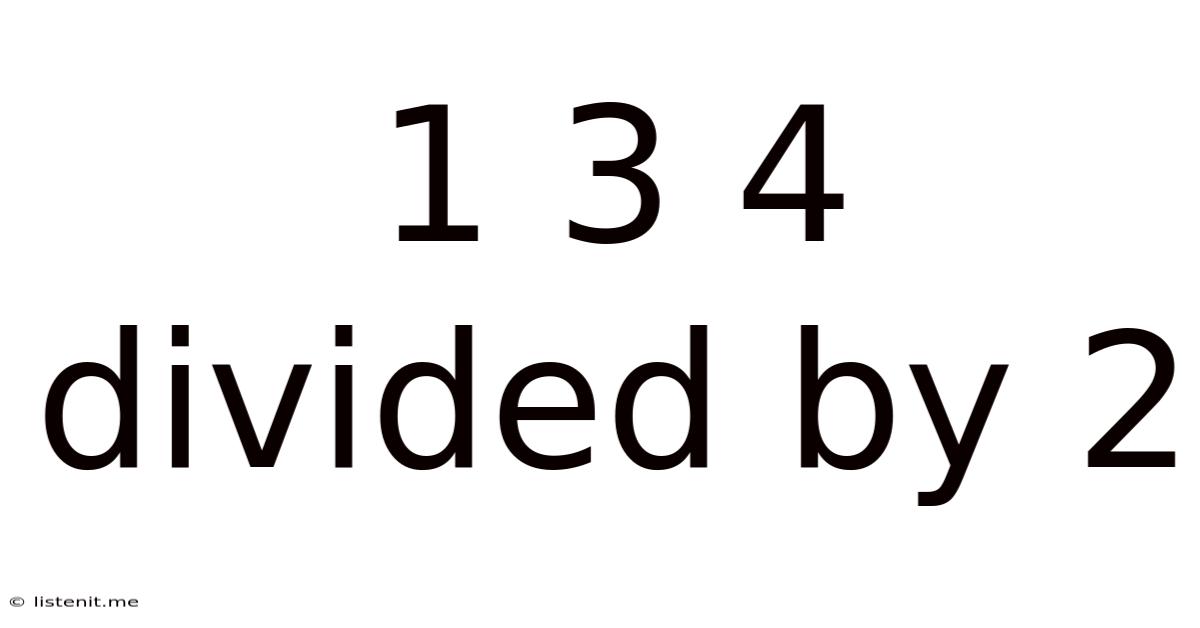
Table of Contents
1 3 4 Divided by 2: A Deep Dive into Mathematical Concepts and Practical Applications
The seemingly simple arithmetic problem, "1 3 4 divided by 2," offers a fascinating gateway to explore several key mathematical concepts and their real-world applications. While the immediate calculation might seem straightforward, a deeper analysis reveals nuances in interpretation, order of operations, and broader implications within various fields. This article will dissect the problem, explore different interpretations, and discuss its relevance in various contexts, from simple arithmetic to more complex mathematical fields.
Understanding the Problem: Interpreting "1 3 4 Divided by 2"
The ambiguity lies in the representation of "1 3 4". Is it a single number (one thousand three hundred and four), a concatenated sequence of digits, or a representation of a more complex mathematical expression? This ambiguity highlights the importance of clear mathematical notation and the potential for misinterpretation.
Interpretation 1: 134 Divided by 2
The most straightforward interpretation is that "1 3 4" represents the number one hundred and thirty-four. In this case, the problem becomes a simple division problem: 134 ÷ 2. The solution is readily obtained through standard division methods:
134 ÷ 2 = 67
This interpretation is likely the intended one for most basic arithmetic contexts. It demonstrates a fundamental operation crucial for numerous everyday applications, from splitting bills evenly to calculating unit costs.
Interpretation 2: A Sequence of Numbers
An alternative interpretation considers "1 3 4" as a sequence of three individual numbers. This interpretation, while unconventional for typical division problems, opens up avenues for exploring different mathematical operations. We could consider several approaches:
-
Division of each number: Dividing each number in the sequence individually by 2: 1 ÷ 2 = 0.5, 3 ÷ 2 = 1.5, 4 ÷ 2 = 2. This approach yields a new sequence: 0.5, 1.5, 2. The meaning and application of this resulting sequence would depend heavily on the context.
-
Concatenation and then division: We could concatenate the sequence to form the number 134 (as in Interpretation 1) and then divide by 2, leading us back to the solution 67.
-
Series Operations: We could potentially treat this sequence as a series and perform operations like summation before division. For example, summing the numbers (1 + 3 + 4 = 8) and then dividing by 2 (8 ÷ 2 = 4) yields a completely different result.
The flexibility of this interpretation underscores the significance of precise mathematical notation and the importance of specifying the intended operation.
Order of Operations (PEMDAS/BODMAS): A Crucial Consideration
When dealing with more complex mathematical expressions, the order of operations (often remembered by the acronyms PEMDAS or BODMAS) plays a pivotal role in ensuring accurate results. PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) and BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) specify the sequence in which operations should be performed.
While "1 3 4 divided by 2" is relatively simple, understanding the order of operations is crucial when dealing with expressions involving multiple operations. For instance, if the problem were presented as something like:
(1 + 3) * 4 ÷ 2
The order of operations would dictate that the parentheses are evaluated first (1 + 3 = 4), then the multiplication (4 * 4 = 16), and finally the division (16 ÷ 2 = 8). A disregard for the order of operations would lead to an incorrect answer.
Beyond Simple Division: Expanding the Scope
The basic division problem, as presented, can be extended into several related mathematical concepts:
Fractions and Decimals
The division operation itself can be represented using fractions or decimals. 134 ÷ 2 can be expressed as the fraction 134/2, which simplifies to 67/1 or simply 67. The decimal representation is 67.0.
Understanding the relationship between fractions, decimals, and division is crucial for comprehending a wide range of mathematical concepts and applications.
Modular Arithmetic
Modular arithmetic, a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value (the modulus), is another area where division plays a significant role. For instance, in modulo 5 arithmetic (working with remainders after division by 5), 134 ÷ 2 would leave a remainder of 4 (since 134 = 2 * 67 + 0). This concept finds significant applications in cryptography and computer science.
Algebraic Equations
The problem can be expanded to form algebraic equations. For example, we could formulate an equation like:
2x = 134
Solving for x involves dividing both sides of the equation by 2, yielding the solution x = 67. This showcases the application of division in solving algebraic problems, a fundamental skill in many mathematical and scientific fields.
Calculus and Analysis
While not directly applicable in a straightforward manner, the principles of division and limits underpin many concepts in calculus and mathematical analysis. The concept of infinitesimals, crucial in calculus, involves division by increasingly smaller numbers, approaching zero.
Real-World Applications: From Everyday Life to Advanced Fields
The seemingly simple problem "1 3 4 divided by 2" finds applications in a surprisingly broad range of contexts:
Everyday Applications:
- Sharing equally: Dividing resources amongst people (splitting a bill, sharing food).
- Unit pricing: Determining the cost of a single item from a bulk purchase.
- Measurement conversions: Converting units (e.g., converting meters to centimeters).
- Recipe scaling: Adjusting ingredient quantities in a recipe.
Scientific and Engineering Applications:
- Physics: Calculating averages, speeds, and other physical quantities.
- Engineering: Designing structures, determining material quantities, and analyzing stresses.
- Chemistry: Calculating concentrations and proportions of substances.
- Computer Science: Data processing, algorithms, and numerical computations.
Financial Applications:
- Investment returns: Calculating rates of return on investments.
- Budgeting: Dividing expenses and income to manage finances.
- Accounting: Analyzing financial statements and calculating ratios.
Improving Mathematical Skills: Practice and Resources
Mastering mathematical concepts, including basic arithmetic operations like division, requires consistent practice and engagement.
- Practice problems: Working through a variety of problems, ranging from simple to complex, is essential to build proficiency.
- Online resources: Numerous online platforms offer interactive exercises and tutorials on various mathematical concepts.
- Seek help when needed: Don't hesitate to seek assistance from teachers, tutors, or online communities when encountering difficulties.
Conclusion: The Unsung Power of Simple Arithmetic
The seemingly trivial problem, "1 3 4 divided by 2," showcases the far-reaching implications of even the most basic mathematical operations. Its analysis reveals the importance of clear notation, a strong understanding of the order of operations, and the broad applications of division in various fields. By understanding and mastering such fundamental concepts, we build a solid foundation for tackling more complex mathematical challenges and applying these skills to real-world problems. The seemingly simple act of dividing 134 by 2 unlocks a world of mathematical possibilities and practical applications, highlighting the inherent power and elegance of mathematics.
Latest Posts
Latest Posts
-
Is Hepatitis And Herpes The Same Thing
Jun 05, 2025
-
What Is A Polar Amino Acid
Jun 05, 2025
-
Spane Scale Of Emotion Research Project
Jun 05, 2025
-
Definition Of Channel Protein In Biology
Jun 05, 2025
-
Castor Oil And The Lymphatic System
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about 1 3 4 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.