1 2 X 2 3 X 3 4
listenit
May 18, 2025 · 5 min read
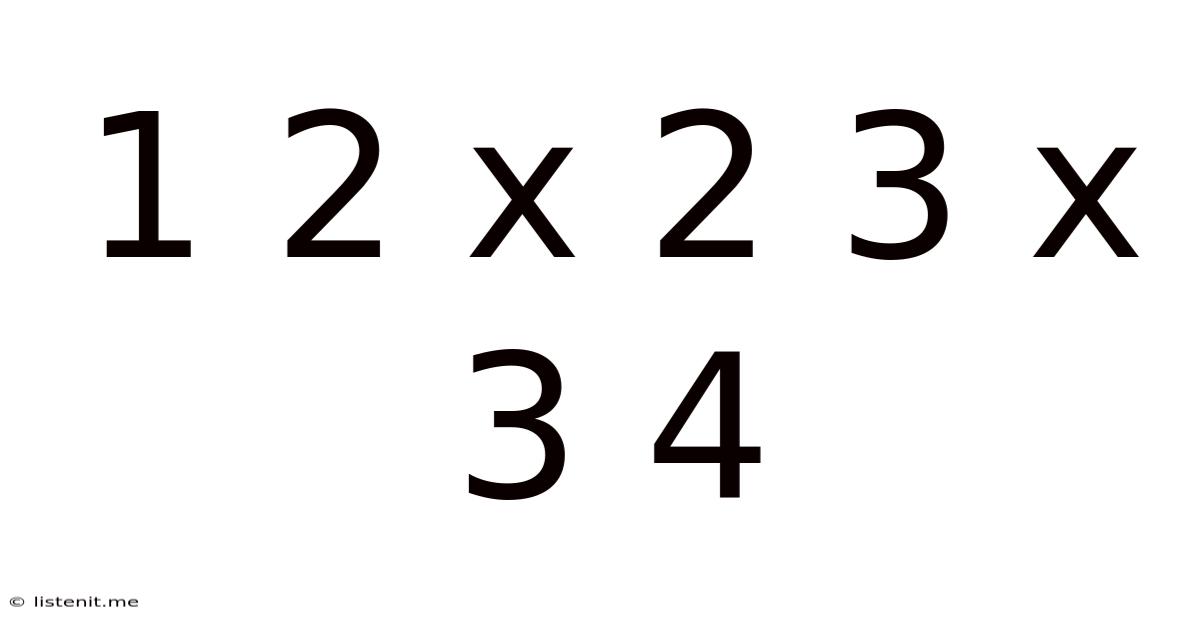
Table of Contents
Decoding the Sequence: 1 2 x 2 3 x 3 4... and the Allure of Mathematical Patterns
The seemingly simple sequence "1 2 x 2 3 x 3 4..." might appear innocuous at first glance. However, beneath its unassuming exterior lies a rich tapestry of mathematical concepts, inviting exploration and sparking curiosity. This article delves deep into this numerical puzzle, investigating its underlying patterns, exploring potential extensions, and uncovering its connections to broader mathematical fields. We'll uncover how understanding this sequence can enhance your problem-solving skills and appreciation for the beauty of mathematics.
Unveiling the Pattern: Multiplication and Progression
The core pattern of the sequence "1 2 x 2 3 x 3 4..." becomes evident upon closer inspection: it interweaves a linear progression of natural numbers (1, 2, 3, 4…) with a multiplicative operation. Specifically, each natural number is immediately followed by itself multiplied by the next consecutive natural number. Let's break it down:
- 1: The first term is simply 1.
- 2 x 2: The second term, 2, is followed by 2 multiplied by the next consecutive number, which is 2 (2 x 2 = 4).
- 3 x 3: Similarly, 3 is followed by 3 multiplied by 4 (3 x 4 = 12).
- 4 x 4: 4 is followed by 4 multiplied by 5 (4 x 5 = 20).
Thus, the extended sequence could be written as: 1, 2, 4, 3, 12, 4, 20, 5, 30, 6, 42, 7, 56… and so on.
Mathematical Foundations: Exploring the Underlying Principles
This seemingly simple sequence touches upon several fundamental mathematical concepts:
1. Natural Numbers: The Building Blocks
The sequence is fundamentally built upon the set of natural numbers, the positive integers (1, 2, 3, 4...). Understanding the properties of natural numbers, such as their infinite nature and their role in counting, is crucial to grasping the sequence’s structure.
2. Arithmetic Progression: The Linear Component
The sequence's linear progression (1, 2, 3, 4...) represents a simple arithmetic progression with a common difference of 1. Arithmetic progressions are characterized by a constant difference between consecutive terms. This linear aspect provides a regular and predictable framework for the sequence.
3. Multiplication: The Core Operation
The multiplication operation is central to the pattern. Understanding the properties of multiplication, including commutativity (a x b = b x a) and associativity (a x (b x c) = (a x b) x c), is essential for extending and manipulating the sequence.
4. Recursive Definition: Generating the Sequence
The sequence can be formally defined recursively. Let's denote the sequence as {a<sub>n</sub>}. We can express it as follows:
- a<sub>1</sub> = 1
- a<sub>2k</sub> = k (where k is a natural number)
- a<sub>2k+1</sub> = k * (k+1) (where k is a natural number)
This recursive definition precisely captures the alternating nature of the sequence, with even-indexed terms representing the linear progression and odd-indexed terms representing the products.
Extending the Sequence: Exploring Further Patterns
The beauty of mathematical sequences lies in their potential for extension and generalization. Let's explore how we might extend this sequence further:
-
Arbitrary Length: The sequence can be extended indefinitely, following the established pattern of alternating between natural numbers and their products with the subsequent natural number. There's no inherent limit to its length.
-
Generalized Pattern: We could generalize the pattern. Instead of multiplying by the next consecutive integer, we could multiply by the integer plus a constant. For example, we could generate a sequence where each number is multiplied by (n+2), resulting in a different pattern.
-
Higher-Order Operations: Instead of simply multiplication, we could incorporate higher-order operations like exponentiation or even more complex mathematical functions to create variations on the initial sequence. This opens up avenues for even more intricate and fascinating patterns.
Applications and Connections: Bridging to Broader Fields
While seemingly simple, the sequence's underlying principles connect to broader mathematical concepts and applications:
1. Number Theory: Divisibility and Factorization
The sequence implicitly involves concepts from number theory, such as divisibility and prime factorization. Analyzing the factors of the product terms (4, 12, 20, etc.) reveals insights into their divisibility properties and prime factors.
2. Combinatorics and Permutations: Counting Possibilities
The sequence could be linked to combinatorics and permutations, exploring the number of ways to arrange elements in a sequence, particularly if variations on the multiplication aspect were introduced.
3. Computer Science and Algorithms: Generating Sequences
Recursive definitions, as demonstrated above, are prevalent in computer science for generating sequences and solving problems efficiently. The sequence provides a straightforward example of implementing a recursive algorithm.
4. Problem-Solving Strategies: Pattern Recognition and Logic
Understanding and extending this sequence hones crucial problem-solving skills, primarily pattern recognition and logical deduction. It demonstrates how seemingly simple patterns can lead to deeper mathematical insights.
Conclusion: The Enduring Allure of Mathematical Exploration
The seemingly simple sequence "1 2 x 2 3 x 3 4..." provides a compelling example of the richness and depth inherent in even the most basic mathematical patterns. Its exploration involves fundamental mathematical concepts, touches upon broader fields, and highlights the importance of pattern recognition and logical deduction. By engaging with such sequences, we develop our mathematical intuition, sharpen our problem-solving abilities, and cultivate an appreciation for the beauty and elegance of mathematics. The ongoing exploration of such patterns continues to inspire mathematical research and reveal the interconnectedness of various mathematical disciplines. The simplicity of the sequence belies its potential for further expansion and application, underscoring the endless possibilities within the realm of mathematical exploration. From recursive definitions to applications in computer science, the sequence provides a fascinating entry point into a world of rich mathematical concepts and discoveries. Further investigation into variations and extensions of this sequence promises to reveal even more intricate patterns and deeper mathematical connections, underscoring the enduring allure of mathematical exploration. The quest to understand, extend, and apply the principles embedded within this seemingly simple sequence exemplifies the ongoing and ever-evolving nature of mathematical discovery.
Latest Posts
Latest Posts
-
Oxidation Of Aldehyde To Carboxylic Acid
Jun 05, 2025
-
How Many People Die From A Colonoscopy
Jun 05, 2025
-
What Is The Neutrality Of Money
Jun 05, 2025
-
What Is Done About A Tortuous Carotid Artery
Jun 05, 2025
-
Should I Have Intercourse After Iui
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about 1 2 X 2 3 X 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.