1 2 Divided By 6 In Fraction Form
listenit
May 25, 2025 · 5 min read
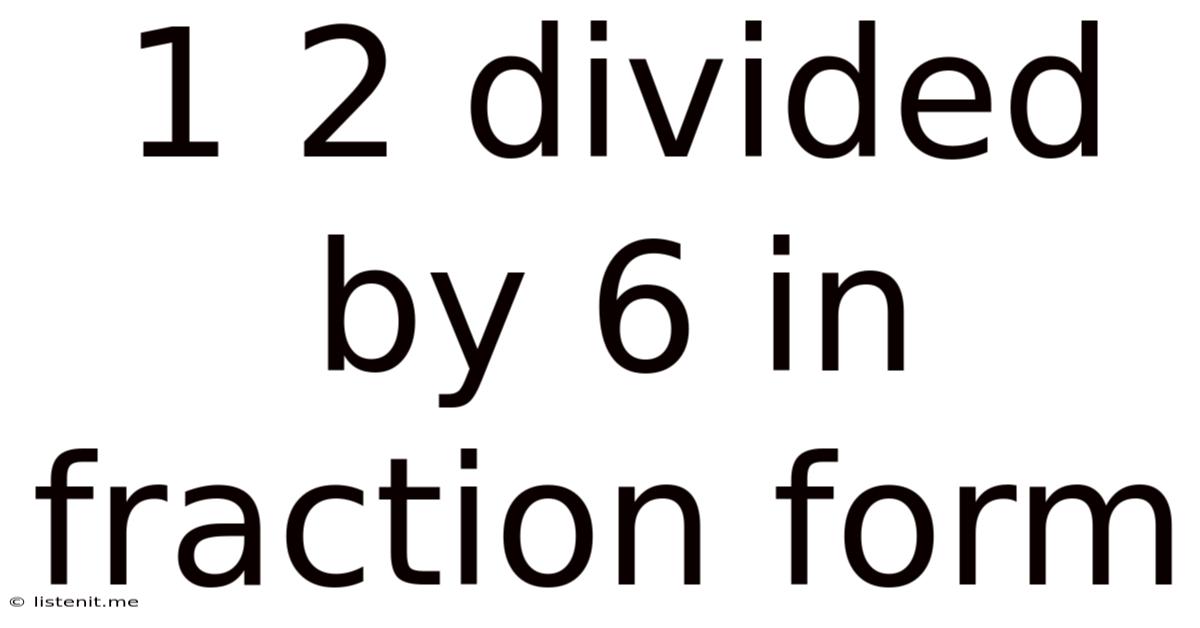
Table of Contents
1/2 Divided by 6: A Deep Dive into Fraction Division
This article will comprehensively explore the seemingly simple problem of dividing one-half (1/2) by six (6), providing a detailed explanation of the process and extending the concepts to broader applications of fraction division. We'll delve into the underlying principles, offer multiple solution methods, and explore real-world scenarios where such calculations might be relevant. By the end, you'll not only understand how to solve this specific problem but also possess a robust understanding of fraction division in general.
Understanding Fraction Division
Before tackling the specific problem of 1/2 ÷ 6, let's establish a solid foundation in fraction division. The core principle revolves around the concept of reciprocals. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2.
Dividing by a fraction is equivalent to multiplying by its reciprocal. This fundamental rule simplifies the process significantly. Instead of directly dividing by a fraction, we can transform the division problem into a multiplication problem by using the reciprocal of the divisor (the number we're dividing by).
The Rule: a/b ÷ c/d = a/b × d/c
This rule applies equally to fractions divided by whole numbers. We simply represent the whole number as a fraction with a denominator of 1. For instance, the number 6 can be written as 6/1.
Solving 1/2 Divided by 6
Now, let's apply this knowledge to our specific problem: 1/2 ÷ 6.
Step 1: Rewrite the whole number as a fraction.
6 can be rewritten as 6/1. Our problem now becomes: 1/2 ÷ 6/1.
Step 2: Apply the reciprocal rule.
To divide by 6/1, we multiply by its reciprocal, which is 1/6. The problem transforms into: 1/2 × 1/6.
Step 3: Multiply the numerators and denominators.
To multiply fractions, we simply multiply the numerators together and the denominators together.
(1 × 1) / (2 × 6) = 1/12
Therefore, 1/2 divided by 6 equals 1/12.
Alternative Methods and Visualizations
While the reciprocal method is the most efficient and commonly used, let's explore alternative approaches to enhance our understanding:
The "Keep, Change, Flip" Method
This mnemonic device helps students remember the steps involved:
- Keep the first fraction the same (1/2).
- Change the division sign to a multiplication sign (×).
- Flip the second fraction (6/1 becomes 1/6).
This leads to the same calculation: 1/2 × 1/6 = 1/12.
Visual Representation
Imagine you have half a pizza (1/2). You want to divide this half pizza equally among six people. Each person would receive a tiny slice, representing 1/12th of the original pizza. This visual aids in understanding the result.
Real-World Applications
Fraction division isn't confined to abstract mathematical exercises. It surfaces in numerous real-world scenarios:
-
Cooking and Baking: Recipes often require dividing ingredients. For example, if a recipe calls for 1/2 cup of sugar and you want to make only 1/6 of the recipe, you'd need to calculate 1/2 ÷ 6 to determine the amount of sugar needed.
-
Construction and Measurement: Dividing lengths or areas into smaller sections frequently involves fraction division. A carpenter might need to divide a 1/2-inch piece of wood into six equal parts.
-
Sharing Resources: If you have half a bag of candy and want to divide it equally among six friends, fraction division helps determine how much candy each person receives.
-
Data Analysis: In statistical analysis or data representation, dividing fractions can be crucial for determining proportions or percentages.
Extending the Concept: Dividing Fractions by Fractions
Let's extend our understanding beyond dividing a fraction by a whole number. Consider dividing a fraction by another fraction. For example, let's solve 2/3 ÷ 1/4.
Step 1: Keep the first fraction (2/3).
Step 2: Change the division sign to multiplication (×).
Step 3: Flip the second fraction (1/4 becomes 4/1).
Step 4: Multiply the fractions: (2/3) × (4/1) = 8/3.
This result, 8/3, is an improper fraction (where the numerator is larger than the denominator). It can be converted to a mixed number: 2 2/3.
Troubleshooting Common Mistakes
When working with fraction division, common pitfalls include:
-
Forgetting to use the reciprocal: The most prevalent mistake is simply dividing the fractions directly without flipping the second fraction. Remember, division by a fraction is multiplication by its reciprocal.
-
Incorrect multiplication of fractions: Carefully multiply the numerators and the denominators. Errors can arise from inaccurate multiplication or addition.
-
Improper simplification: Always simplify the resulting fraction to its lowest terms. For instance, 2/4 can be simplified to 1/2.
Practice Problems
To solidify your understanding, try these practice problems:
- 3/4 ÷ 2
- 1/3 ÷ 1/2
- 2/5 ÷ 4/5
- 5/8 ÷ 10
- 1/6 ÷ 1/3
Conclusion
Dividing fractions, even seemingly simple problems like 1/2 ÷ 6, requires a firm grasp of the principles of reciprocals and fraction multiplication. By understanding the underlying concepts and practicing different solution methods, you'll build confidence and proficiency in tackling various fraction division problems. Remember to always approach these problems methodically, applying the "keep, change, flip" method or the reciprocal rule consistently. This will ensure accuracy and promote a strong understanding of this fundamental mathematical operation with extensive real-world applications. Regular practice is key to mastering fraction division and applying this skill confidently in diverse contexts.
Latest Posts
Latest Posts
-
What Is 2 5 Of 40
May 25, 2025
-
What Year Were You Born If Your 19 In 2024
May 25, 2025
-
Born In 1989 How Old Are You
May 25, 2025
-
Born In 1962 How Old Am I
May 25, 2025
-
10 Is What Percent Of 19
May 25, 2025
Related Post
Thank you for visiting our website which covers about 1 2 Divided By 6 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.