1/2 Divided By 4 As A Fraction
listenit
May 24, 2025 · 5 min read
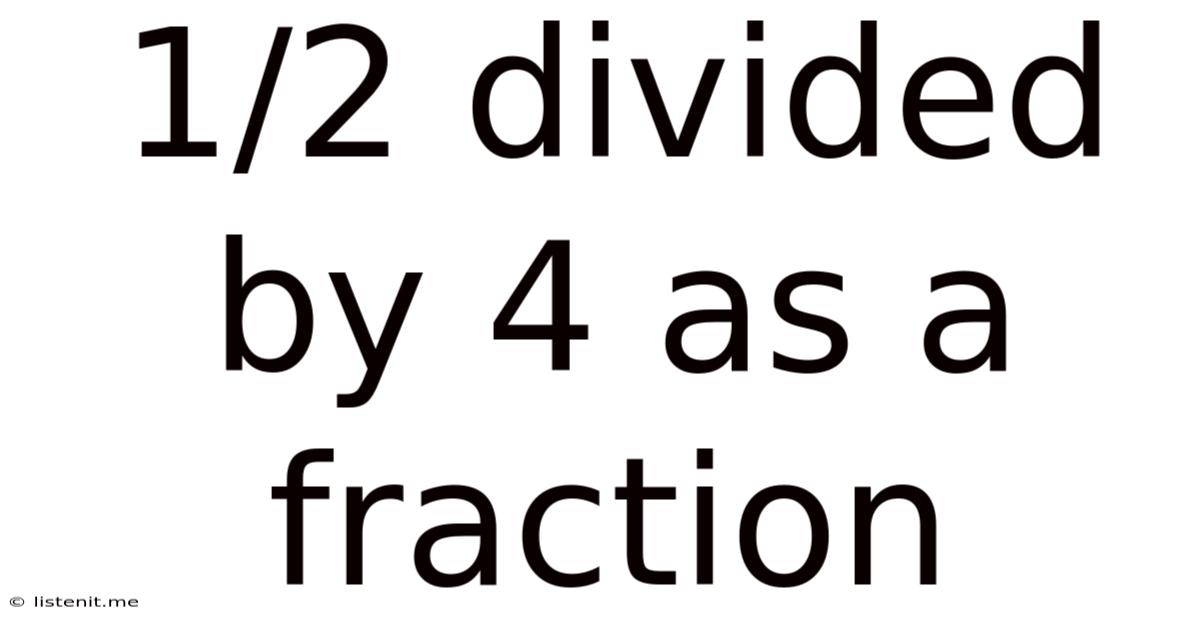
Table of Contents
1/2 Divided by 4: A Deep Dive into Fraction Division
Understanding fraction division can be tricky, but it's a fundamental concept in mathematics with wide-ranging applications. This comprehensive guide will dissect the problem of 1/2 divided by 4, explaining the process step-by-step, exploring various methods, and providing real-world examples to solidify your understanding. We'll delve into the underlying principles, ensuring you not only get the answer but also grasp the "why" behind the calculations.
Understanding Fraction Division
Before tackling 1/2 divided by 4, let's review the basics of dividing fractions. The core concept revolves around the idea of reciprocals (also known as multiplicative inverses). The reciprocal of a fraction is obtained by swapping its numerator and denominator. For example, the reciprocal of 2/3 is 3/2.
Dividing by a fraction is equivalent to multiplying by its reciprocal. This is the cornerstone of solving fraction division problems. The general rule is:
a/b ÷ c/d = a/b x d/c
Where 'a', 'b', 'c', and 'd' represent numbers, and 'b' and 'c' are not zero (division by zero is undefined).
Solving 1/2 Divided by 4
Now, let's apply this principle to our specific problem: 1/2 divided by 4. First, we need to represent 4 as a fraction. Any whole number can be written as a fraction with a denominator of 1. Therefore, 4 can be written as 4/1.
Our problem now becomes:
1/2 ÷ 4/1
Following the rule of fraction division, we change the division operation to multiplication by taking the reciprocal of the second fraction:
1/2 x 1/4
To multiply fractions, we simply multiply the numerators together and the denominators together:
(1 x 1) / (2 x 4) = 1/8
Therefore, 1/2 divided by 4 is equal to 1/8.
Alternative Methods and Visual Representations
While the reciprocal method is the most efficient, let's explore other approaches to visualize and understand the process.
Using Visual Models
Imagine you have half a pizza (1/2). You want to divide this half pizza equally among four people. How much pizza does each person get? You would need to divide the half pizza into four equal slices. Each slice represents 1/8 of the whole pizza. This visual representation confirms our calculated answer of 1/8.
The "Keep, Change, Flip" Method
This mnemonic is a popular way to remember how to divide fractions. It stands for:
- Keep the first fraction as it is.
- Change the division sign to a multiplication sign.
- Flip (find the reciprocal of) the second fraction.
Applying this to our problem:
- Keep: 1/2
- Change: ÷ becomes x
- Flip: 4/1 becomes 1/4
This leads us to the same multiplication problem: 1/2 x 1/4 = 1/8
Real-World Applications
Understanding fraction division is crucial in various real-world scenarios. Here are some examples:
- Baking: A recipe calls for 1/2 cup of flour, but you want to make only 1/4 of the recipe. You need to calculate 1/2 cup ÷ 4 = 1/8 cup of flour.
- Sharing Resources: You have 1/2 of a bag of candy, and you want to share it equally among 4 friends. Each friend gets 1/8 of the bag.
- Measurement and Construction: In construction or engineering, precise measurements are critical. Dividing fractional measurements is common practice. For instance, you might need to divide a length of wood that is 1/2 a meter into 4 equal pieces.
- Financial Calculations: Dividing fractional shares of stocks or calculating portions of investment returns often involves fraction division.
Expanding the Understanding: Dividing Fractions with Larger Numbers
Let's extend our understanding by solving similar problems involving larger numbers to solidify the concept of fraction division.
Example 1: 3/4 divided by 6
First, represent 6 as a fraction: 6/1. Then apply the reciprocal method:
3/4 ÷ 6/1 = 3/4 x 1/6 = (3 x 1) / (4 x 6) = 3/24
This fraction can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 3:
3/24 = 1/8
Therefore, 3/4 divided by 6 is equal to 1/8.
Example 2: 5/6 divided by 2/3
Apply the reciprocal method:
5/6 ÷ 2/3 = 5/6 x 3/2 = (5 x 3) / (6 x 2) = 15/12
This fraction can be simplified to 5/4 or 1 1/4.
Therefore, 5/6 divided by 2/3 is equal to 5/4 or 1 1/4.
Addressing Common Mistakes and Troubleshooting
While the process of dividing fractions seems straightforward, some common mistakes can lead to incorrect answers. Let’s address these:
- Forgetting to find the reciprocal: This is perhaps the most common error. Remember, you must take the reciprocal of the second fraction before multiplying.
- Incorrect multiplication: Carefully multiply the numerators and the denominators separately. Double-check your calculations.
- Not simplifying the fraction: Always simplify the resulting fraction to its lowest terms to provide the most concise answer.
Conclusion: Mastering Fraction Division
Mastering fraction division is a crucial skill that extends beyond the classroom. By understanding the concept of reciprocals, utilizing the "keep, change, flip" method, and practicing with various examples, you can confidently tackle any fraction division problem. Remember to visualize the problem when possible, use visual aids like diagrams, and always double-check your calculations to avoid errors. The more you practice, the more intuitive this process will become, making it an invaluable tool in various mathematical and real-world situations. This in-depth explanation of 1/2 divided by 4 provides a strong foundation for tackling more complex fraction problems with greater confidence and understanding.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 90 And 135
May 25, 2025
-
17 Out Of 22 Is What Percent
May 25, 2025
-
One Percent Of A Million Dollars
May 25, 2025
-
Whats The Prime Factorization Of 27
May 25, 2025
-
Usable Ip Addresses In A 30
May 25, 2025
Related Post
Thank you for visiting our website which covers about 1/2 Divided By 4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.