1/2 Divided By 3/4 In A Fraction
listenit
May 18, 2025 · 5 min read
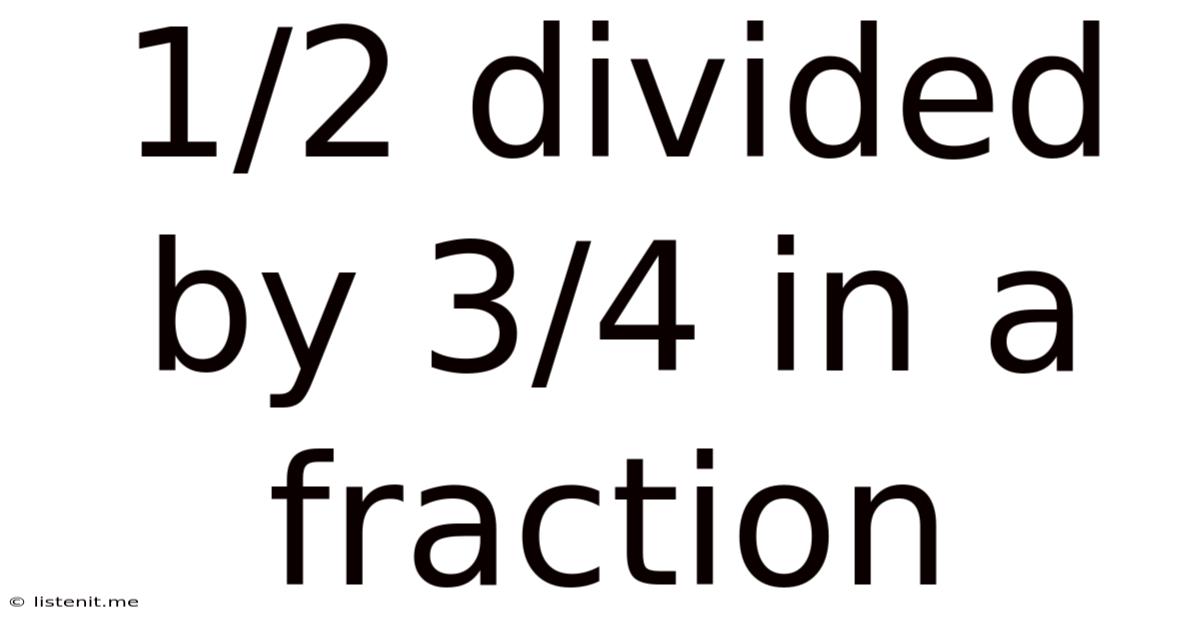
Table of Contents
1/2 Divided by 3/4: A Deep Dive into Fraction Division
Dividing fractions can seem daunting at first, but with a clear understanding of the process and a bit of practice, it becomes straightforward. This comprehensive guide will walk you through dividing 1/2 by 3/4, explaining the underlying principles and providing you with various approaches to solve this type of problem. We'll explore different methods, delve into the reasoning behind each step, and even look at real-world applications to solidify your understanding.
Understanding Fraction Division: The "Keep, Change, Flip" Method
The most common method for dividing fractions is the "keep, change, flip" (or "keep, switch, flip") method. This catchy phrase simplifies the process, but let's break down why it works.
The Core Principle: Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 3/4 is 4/3.
Applying the Method:
- Keep: Keep the first fraction exactly as it is: 1/2.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second fraction (find its reciprocal): 3/4 becomes 4/3.
Therefore, 1/2 ÷ 3/4 becomes 1/2 × 4/3.
Calculating the Result:
Now, we simply multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(1 × 4) / (2 × 3) = 4/6
Simplifying the Fraction:
Finally, we simplify the resulting fraction by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 4 and 6 is 2. Dividing both the numerator and the denominator by 2, we get:
4/6 = 2/3
Therefore, 1/2 divided by 3/4 is 2/3.
Visualizing Fraction Division with Models
Understanding fraction division can be enhanced by visualizing the problem using models. Imagine you have 1/2 of a pizza. You want to divide this half-pizza into portions that are each 3/4 the size of a whole pizza. How many portions will you have?
This illustrates the concept of dividing a fraction by a fraction. You're essentially asking: "How many 3/4-sized portions fit into a 1/2-sized portion?" The answer, as we calculated above, is 2/3 of a portion. It means that you can fit two-thirds of a 3/4-sized portion into a 1/2-sized portion. While not a perfect whole number, it clearly demonstrates the result obtained through the mathematical calculation.
Alternative Methods: Understanding the Underlying Mathematics
While the "keep, change, flip" method is efficient, understanding the underlying mathematical principles provides a deeper grasp of fraction division.
Method 1: Using Complex Fractions
We can express the division problem as a complex fraction:
(1/2) / (3/4)
To simplify a complex fraction, we multiply the numerator by the reciprocal of the denominator:
(1/2) × (4/3) = 4/6 = 2/3
This method directly applies the principle of dividing by a fraction being equivalent to multiplying by its reciprocal.
Method 2: Finding a Common Denominator
Another approach involves finding a common denominator for both fractions before dividing. The least common denominator (LCD) of 2 and 4 is 4. We rewrite the fractions with this common denominator:
(1/2) ÷ (3/4) = (2/4) ÷ (3/4)
Now, we can focus solely on the numerators:
2 ÷ 3 = 2/3
This method shows that dividing fractions with the same denominator is essentially dividing the numerators.
Real-World Applications of Fraction Division
Fraction division isn't just a theoretical exercise; it appears frequently in everyday situations. Here are a few examples:
-
Cooking: A recipe calls for 3/4 cup of flour, but you only want to make half the recipe. How much flour do you need? You'd divide 3/4 by 2 (or multiply by 1/2): (3/4) ÷ 2 = 3/8 cup of flour.
-
Sewing: You have 1/2 yard of fabric and need to cut pieces that are each 3/4 of a yard long. How many pieces can you cut? This is directly analogous to our problem: (1/2) ÷ (3/4) = 2/3 of a piece. You can't cut a full piece, but a fraction of one.
-
Construction: You need to divide a 1/2-mile section of road into segments that are each 3/4 of a mile long. How many segments will there be? (1/2) ÷ (3/4) = 2/3. This implies that the 1/2 mile section is only two-thirds the length of the intended segment size.
-
Time Management: You have 1/2 an hour to complete three tasks. If you allot an equal amount of time to each task, how long will you spend on each? You would divide 1/2 by 3: (1/2) ÷ 3 = 1/6 of an hour per task.
These examples illustrate that fraction division is a practical skill applicable to various contexts.
Mastering Fraction Division: Practice and Further Exploration
The key to mastering fraction division, like any mathematical skill, is practice. Start with simple examples and gradually increase the complexity of the fractions involved. There are countless online resources, worksheets, and practice problems available to help you hone your skills.
Furthermore, exploring different methods of solving fraction division problems will deepen your understanding and help you choose the most efficient method depending on the problem's context. Don't hesitate to experiment and find the approach that resonates best with your learning style.
Conclusion: Confidence in Fraction Division
Dividing fractions, while initially appearing challenging, becomes manageable with the right understanding and practice. The "keep, change, flip" method provides a simple yet powerful approach. Understanding the underlying principles through alternative methods like using complex fractions or finding a common denominator enhances your overall mathematical comprehension. By practicing regularly and applying your knowledge to real-world scenarios, you'll build confidence and proficiency in tackling fraction division problems with ease. Remember, the more you practice, the more intuitive and straightforward this process will become. You'll find yourself effortlessly solving fraction division problems in various contexts and applying this crucial skill to a range of situations in your daily life and studies.
Latest Posts
Latest Posts
-
Is Hepatitis And Herpes The Same Thing
Jun 05, 2025
-
What Is A Polar Amino Acid
Jun 05, 2025
-
Spane Scale Of Emotion Research Project
Jun 05, 2025
-
Definition Of Channel Protein In Biology
Jun 05, 2025
-
Castor Oil And The Lymphatic System
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about 1/2 Divided By 3/4 In A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.