1 2 3 Divided By 1 8
listenit
May 18, 2025 · 5 min read
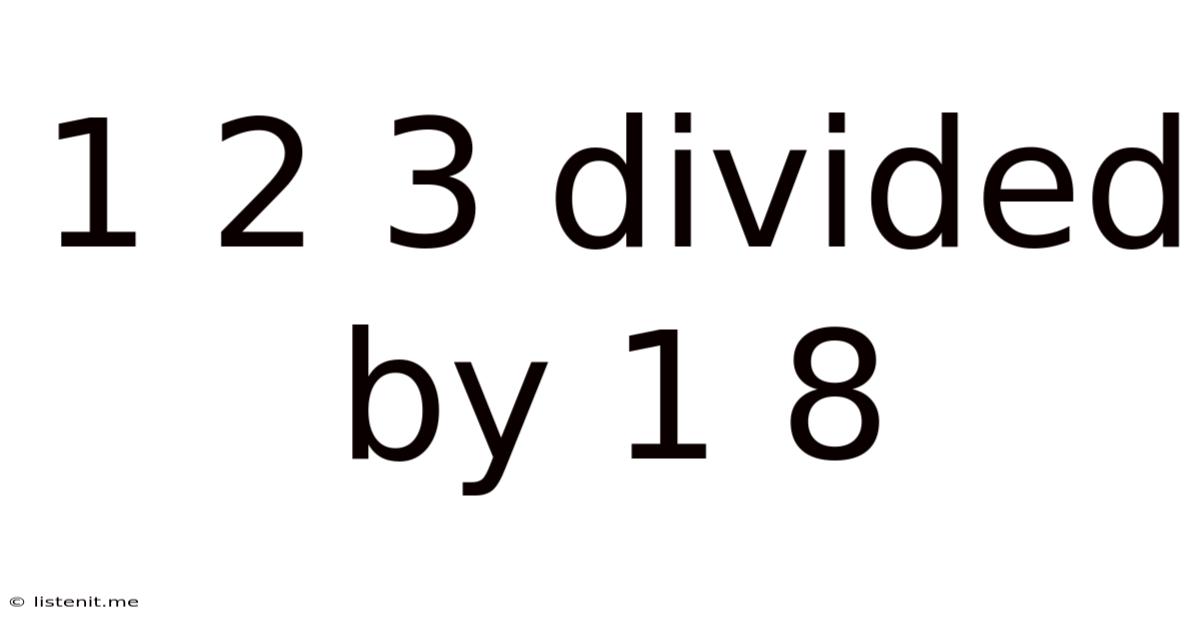
Table of Contents
Decoding 1 2 3 Divided by 1 8: A Deep Dive into Mathematical Operations and Their Applications
The seemingly simple question of "1 2 3 divided by 1 8" presents a fascinating opportunity to explore several key mathematical concepts. At first glance, it might appear straightforward, but delving deeper reveals nuances in interpreting the notation, performing the calculation, and understanding its broader implications in various fields. This article aims to provide a comprehensive analysis of this problem, covering diverse aspects from basic arithmetic to advanced mathematical principles and real-world applications.
Understanding the Notation: The Importance of Clarity
Before we even begin the calculation, it's crucial to address the ambiguous nature of the notation "1 2 3 divided by 1 8." This phrasing lacks the precision required for unambiguous mathematical expression. To clarify, we need to consider two possible interpretations:
1. Concatenated Numbers: The "1 2 3" and "1 8" could represent the concatenated numbers 123 and 18. In this case, the problem becomes 123 ÷ 18.
2. Separate Numbers: Alternatively, "1 2 3" could represent three separate numbers, and similarly for "1 8." This interpretation, however, requires further clarification about the intended operation. Are we to sum the numbers before division, or perhaps perform a different operation? This ambiguity necessitates a clear definition before proceeding.
For the remainder of this article, we will focus on the most likely and straightforward interpretation: 123 divided by 18 (123 ÷ 18). This allows for a clear and comprehensive exploration of the associated mathematical concepts.
Performing the Division: Methods and Results
The division of 123 by 18 can be performed using several methods:
1. Long Division: The traditional long division method provides a step-by-step process.
6
18 | 123
-108
15
This reveals that 123 divided by 18 is 6 with a remainder of 15. This can be expressed as a mixed number (6 15/18) or a decimal (6.8333...).
2. Calculator: A calculator provides a quick and efficient way to obtain the result. Simply inputting 123 ÷ 18 will yield the decimal approximation of 6.8333...
3. Fractions: Expressing the result as a fraction is also possible. The remainder of 15 over the divisor 18 gives us 15/18. This fraction can be simplified by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 3. This simplification results in the equivalent fraction 5/6. Therefore, 123/18 simplifies to 6 and 5/6.
Extending the Concepts: Exploring Related Mathematical Ideas
The seemingly simple division problem opens doors to a wide range of mathematical concepts:
1. Decimals and Fractions: The division highlights the relationship between decimals and fractions. The decimal approximation (6.8333...) is equivalent to the mixed number 6 5/6. Understanding this equivalence is fundamental in various mathematical applications.
2. Remainders and Modular Arithmetic: The remainder of 15 when dividing 123 by 18 introduces the concept of modular arithmetic. In modular arithmetic (modulo 18), 123 is congruent to 15 (123 ≡ 15 (mod 18)). This concept has wide applications in cryptography, computer science, and other fields.
3. Prime Factorization: Examining the prime factorization of 123 (3 x 41) and 18 (2 x 3 x 3) can offer insights into the divisibility properties of the numbers involved. Understanding prime factorization is crucial in simplifying fractions and solving more complex mathematical problems.
4. Greatest Common Divisor (GCD) and Least Common Multiple (LCM): Finding the GCD and LCM of 123 and 18 is useful in various mathematical operations, including simplifying fractions and solving problems involving ratios and proportions. The GCD of 123 and 18 is 3, while the LCM is 981.
Real-World Applications: Connecting Math to Practical Scenarios
The principles illustrated by this simple division problem have extensive practical applications across multiple domains:
1. Division of Resources: Imagine dividing 123 apples among 18 people. Each person would receive 6 apples, with 15 apples remaining. This practical application shows the relevance of remainders in real-world scenarios.
2. Financial Calculations: Dividing a total cost among a group of people, calculating unit prices, or determining profit margins all involve similar division processes. Understanding these calculations is crucial in personal finance and business management.
3. Engineering and Physics: Many engineering and physics calculations involve division. For example, calculating speeds, forces, and ratios frequently requires division operations. The precision and understanding of remainders are crucial for accurate results.
4. Computer Science: Division operations form the backbone of numerous algorithms and processes in computer science. From simple arithmetic to complex calculations, understanding division is essential for programming and software development.
Beyond the Basics: Exploring Advanced Concepts
The initial problem, while seemingly simple, can serve as a stepping stone to more advanced mathematical concepts:
1. Continued Fractions: The decimal representation of 123/18 (6.8333...) can be expressed as a continued fraction, offering a different way to represent the result and explore its properties.
2. Approximations and Error Analysis: When dealing with decimals, understanding the concept of approximations and analyzing the associated error becomes essential, particularly in applications where precision is critical.
3. Abstract Algebra: The concepts of remainders and modular arithmetic form a foundation for abstract algebra, a branch of mathematics dealing with abstract algebraic structures.
Conclusion: The Power of Simple Problems
The seemingly simple problem of 123 divided by 18 has led us on a journey through various mathematical concepts and their real-world applications. This underscores the power of simple problems in unlocking a deeper understanding of mathematical principles and their relevance in our daily lives. By carefully examining the notation, performing the calculation, and exploring related concepts, we can appreciate the interconnectedness of mathematical ideas and their profound impact across various fields. The seemingly simple act of division holds within it a universe of mathematical richness, highlighting the beauty and power of mathematics in its most fundamental forms. Further exploration into these areas will only deepen one's appreciation for the elegance and utility of mathematics in solving real-world challenges.
Latest Posts
Latest Posts
-
What Are The Consequences Of Having Pyrimidine Dimers In Dna
Jun 05, 2025
-
Does Pi Rads 5 Mean Aggressive Cancer
Jun 05, 2025
-
Is Hepatitis And Herpes The Same Thing
Jun 05, 2025
-
What Is A Polar Amino Acid
Jun 05, 2025
-
Spane Scale Of Emotion Research Project
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about 1 2 3 Divided By 1 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.