1 12 Divided By 2 3
listenit
May 24, 2025 · 5 min read
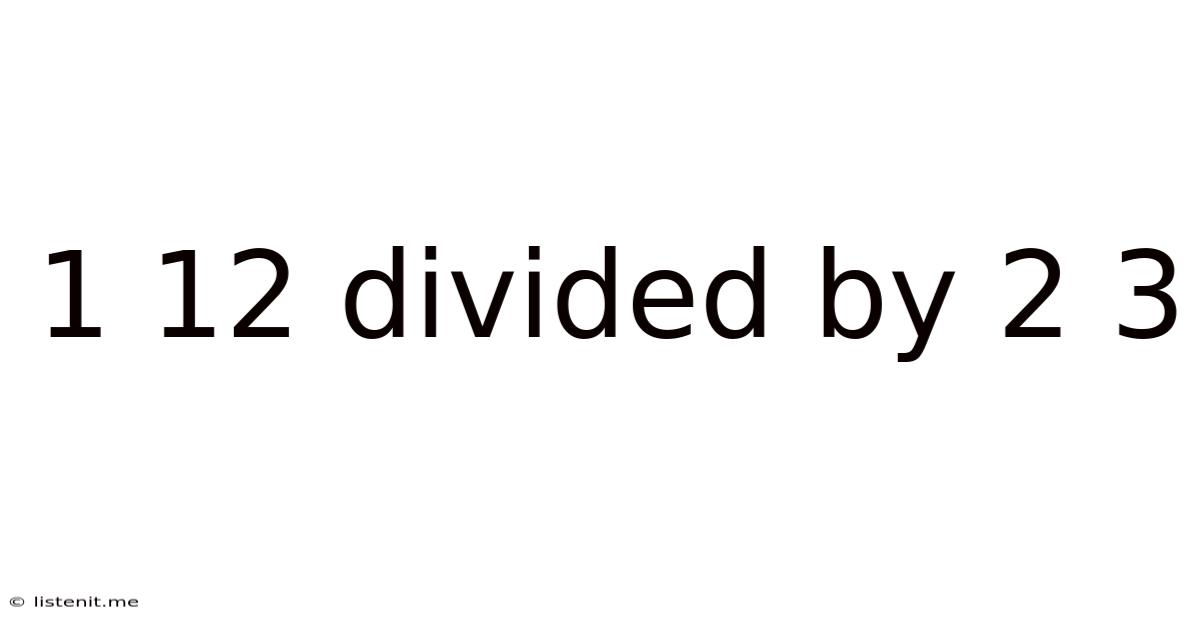
Table of Contents
112 Divided by 23: A Deep Dive into Division and its Applications
The seemingly simple question, "What is 112 divided by 23?", opens a door to a fascinating exploration of division, its various methods, and its wide-ranging applications in mathematics and beyond. This isn't just about finding a numerical answer; it's about understanding the underlying principles and appreciating the significance of this fundamental arithmetic operation.
Understanding Division: More Than Just Sharing
Division, at its core, is the inverse operation of multiplication. While multiplication combines quantities, division separates a quantity into equal parts. Think of it as sharing: if you have 112 cookies and want to share them equally among 23 friends, division tells you how many cookies each friend receives.
The components of a division problem are:
- Dividend: The number being divided (112 in this case). This represents the total quantity being shared.
- Divisor: The number by which the dividend is divided (23). This represents the number of equal parts or groups.
- Quotient: The result of the division. This is the number of items in each group.
- Remainder: The amount left over after the division if the dividend is not perfectly divisible by the divisor.
Methods for Dividing 112 by 23
Several methods can be employed to solve 112 ÷ 23:
1. Long Division: The Classic Approach
Long division is a standard algorithm taught in schools. It systematically breaks down the division into smaller, manageable steps.
4
23 | 112
-92
20
Following these steps:
- Divide: How many times does 23 go into 11? It doesn't go at all, so we consider 112. 23 goes into 112 approximately 4 times (23 x 4 = 92).
- Multiply: Multiply the quotient (4) by the divisor (23): 4 x 23 = 92.
- Subtract: Subtract the product (92) from the dividend (112): 112 - 92 = 20.
- Remainder: The remainder is 20.
Therefore, 112 divided by 23 is 4 with a remainder of 20. This can be expressed as 4 R 20 or 4 + 20/23.
2. Repeated Subtraction: A Conceptual Approach
Repeated subtraction is a more intuitive method, particularly helpful for visualizing the division process. We repeatedly subtract the divisor from the dividend until we reach a value less than the divisor.
- 112 - 23 = 89
- 89 - 23 = 66
- 66 - 23 = 43
- 43 - 23 = 20
We subtracted 23 four times before reaching a remainder of 20. This reinforces the result obtained through long division.
3. Using a Calculator: The Quickest Method
For practical purposes, a calculator offers the fastest and most efficient way to perform the division. Simply input 112 ÷ 23, and the calculator will return the result, often displaying it as a decimal: approximately 4.8696.
Interpreting the Results: Quotient and Remainder
The result of 112 ÷ 23, whether expressed as 4 R 20 or approximately 4.87, requires careful interpretation depending on the context.
- Whole Number Quotient (4): This represents the number of complete groups that can be formed. In our cookie example, each of the 23 friends would receive 4 cookies.
- Remainder (20): This represents the leftover amount that cannot be equally distributed. In our cookie example, there would be 20 cookies remaining.
- Decimal Quotient (4.87): This represents the average number of cookies per friend, considering the leftover cookies are divided fractionally. This interpretation is useful when dealing with situations where fractional parts are meaningful (e.g., dividing a quantity of liquid).
Real-World Applications of Division: Beyond Cookies
Division isn't confined to simple sharing problems. It's a fundamental operation with wide-ranging applications across various fields:
- Finance: Calculating per-unit costs, splitting bills, determining profit margins, and calculating interest rates all involve division.
- Engineering: Designing structures, calculating material quantities, and determining optimal ratios are all dependent on precise division calculations.
- Computer Science: Division plays a crucial role in algorithms, data structures, and programming logic. Many computational processes depend on efficient division operations.
- Science: Analyzing experimental data, calculating concentrations, and converting units often require division.
- Everyday Life: Sharing resources, measuring ingredients in cooking, dividing tasks, and calculating travel times frequently involve division.
Advanced Applications: Fractions and Decimals
The remainder from a division problem can be expressed as a fraction (20/23) or a decimal (approximately 0.87). This expands the application of division to situations requiring fractional or decimal results. The ability to work with fractions and decimals is vital in more complex mathematical operations.
Understanding how to handle remainders is critical. Sometimes the remainder is simply a leftover quantity; other times, it needs to be incorporated into the overall solution. The context dictates how the remainder is handled.
Exploring Related Mathematical Concepts
The division problem 112 ÷ 23 is also an opportunity to explore related mathematical concepts:
- Factors and Multiples: Understanding factors and multiples helps in estimating the quotient before performing the division.
- Prime Factorization: Breaking down numbers into their prime factors provides insight into divisibility.
- Greatest Common Divisor (GCD) and Least Common Multiple (LCM): These concepts are fundamental in simplifying fractions and solving problems involving ratios and proportions.
- Modular Arithmetic: The remainder obtained in a division problem is the foundation of modular arithmetic, a powerful tool in cryptography and number theory.
Conclusion: The Enduring Importance of Division
The seemingly simple problem of 112 divided by 23 offers a profound glimpse into the power and versatility of division. From the fundamental steps of long division to the sophisticated applications in various fields, division remains an indispensable mathematical operation. Mastering division is not just about finding answers; it's about developing a deeper understanding of numerical relationships and problem-solving skills that extend far beyond the classroom. The ability to interpret results, handle remainders effectively, and apply division in diverse contexts are crucial skills for success in various areas of life. This detailed exploration highlights the enduring importance of this foundational arithmetic operation.
Latest Posts
Latest Posts
-
One Hour And 30 Minutes From Now
May 24, 2025
-
What Is The Greatest Common Factor Of 18 And 81
May 24, 2025
-
If I Was Born 1965 How Old Am I
May 24, 2025
-
How Long Is 5 Years In Days
May 24, 2025
-
Calories Burned Calculator By Heart Rate
May 24, 2025
Related Post
Thank you for visiting our website which covers about 1 12 Divided By 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.