1 1 2 Divided By 1 2
listenit
May 18, 2025 · 5 min read
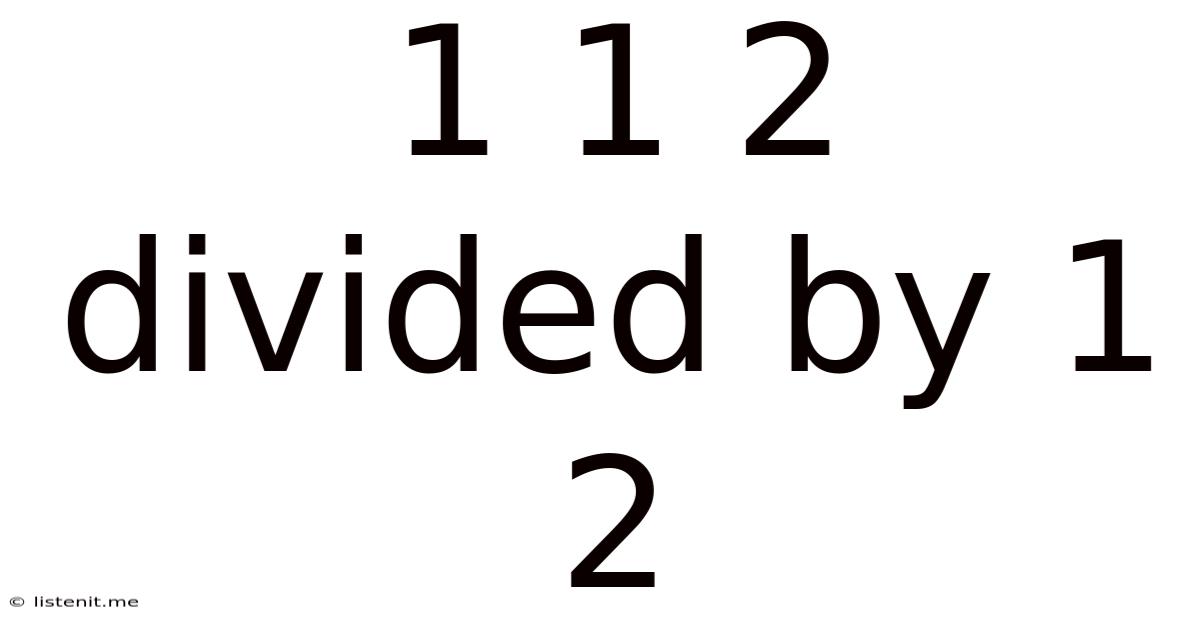
Table of Contents
1 1/2 Divided by 1/2: A Deep Dive into Fraction Division
Understanding fraction division can be a stumbling block for many, but mastering it unlocks a world of mathematical possibilities. This comprehensive guide will dissect the problem of 1 1/2 divided by 1/2, exploring not only the solution but also the underlying principles and various methods for solving similar problems. We’ll delve into the practical applications and explore how this seemingly simple calculation can be applied in real-world scenarios.
Understanding Fractions: A Foundation for Division
Before tackling the division, let's solidify our understanding of fractions. A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator shows how many equal parts the whole is divided into.
For instance, in the fraction 1/2, the numerator (1) indicates one part, and the denominator (2) signifies that the whole is divided into two equal parts. Therefore, 1/2 represents one-half of a whole.
Mixed numbers, like 1 1/2, combine a whole number and a fraction. 1 1/2 means one whole unit plus one-half of another unit. To work effectively with mixed numbers in division, it's often beneficial to convert them into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
Converting Mixed Numbers to Improper Fractions
To convert 1 1/2 into an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 1 * 2 = 2
- Add the numerator to the result: 2 + 1 = 3
- Keep the same denominator: The denominator remains 2.
Therefore, 1 1/2 is equivalent to the improper fraction 3/2.
Diving into the Division: 1 1/2 ÷ 1/2
Now, we can rewrite our problem using the improper fraction: 3/2 ÷ 1/2. Dividing fractions involves a crucial concept: reciprocals. The reciprocal of a fraction is obtained by swapping the numerator and the denominator.
For example, the reciprocal of 1/2 is 2/1 (or simply 2).
The "Keep, Change, Flip" Method
One of the most common and intuitive methods for dividing fractions is the "keep, change, flip" method:
- Keep: Keep the first fraction as it is (3/2).
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip (find the reciprocal of) the second fraction (1/2 becomes 2/1).
This transforms our problem into: 3/2 × 2/1
Multiplying Fractions
Multiplying fractions is straightforward: multiply the numerators together and multiply the denominators together.
(3 × 2) / (2 × 1) = 6/2
Simplifying the Result
The fraction 6/2 can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 2.
6/2 = 3/1 = 3
Therefore, 1 1/2 divided by 1/2 equals 3.
Alternative Methods for Fraction Division
While the "keep, change, flip" method is highly popular, other methods can also be used to solve fraction division problems. Understanding these alternatives can deepen your understanding of the underlying mathematical principles.
Method 2: Using the Common Denominator
This method involves converting both fractions to have a common denominator before dividing. In our case, both fractions already have a denominator of 2, so we can proceed directly to division:
(3/2) ÷ (1/2) = (3/2) × (2/1) = 6/2 = 3
This method highlights that dividing by a fraction is essentially multiplying by its reciprocal, even without explicitly applying the "keep, change, flip" rule.
Real-World Applications of Fraction Division
Fraction division isn't just a theoretical concept; it's frequently applied in various real-world situations:
-
Cooking and Baking: Dividing recipes to accommodate smaller portions often involves fraction division. For instance, if a recipe calls for 1 1/2 cups of flour and you want to halve the recipe, you'd divide 1 1/2 by 1/2 to determine the amount of flour needed.
-
Sewing and Crafting: Calculating fabric requirements or dividing materials for crafting projects frequently uses fraction division to ensure accurate measurements.
-
Construction and Engineering: Precise measurements are crucial in these fields, and fraction division helps in accurately dividing lengths, volumes, or areas.
-
Data Analysis: Understanding proportions and ratios, often represented as fractions, is essential in many types of data analysis, and division of fractions is critical for calculations and interpretations.
Troubleshooting Common Mistakes in Fraction Division
Several common mistakes can occur when dividing fractions. Understanding these pitfalls can prevent errors and improve accuracy:
-
Forgetting to find the reciprocal: One of the most common errors is failing to find the reciprocal of the second fraction before multiplying. Always remember the "keep, change, flip" rule.
-
Incorrectly multiplying or simplifying: Ensure that you correctly multiply the numerators and denominators and then simplify the resulting fraction to its lowest terms.
-
Improper conversion of mixed numbers: Before proceeding with the division, always accurately convert mixed numbers into improper fractions. An error in this step will propagate throughout the calculation.
-
Misunderstanding the concept of reciprocals: Make sure you fully understand what a reciprocal is and how to find it. This is the cornerstone of fraction division.
Advanced Applications and Extensions
The principles of fraction division extend beyond simple calculations. They form the basis for more complex mathematical operations, including:
-
Algebraic Fractions: Fraction division is fundamental in solving algebraic equations involving fractions.
-
Calculus: Derivatives and integrals, core concepts in calculus, often involve manipulating and simplifying fractional expressions.
-
Higher-level Mathematics: Fraction division plays a role in various branches of advanced mathematics, from linear algebra to complex analysis.
Conclusion: Mastering Fraction Division
Understanding fraction division is crucial for success in mathematics and its many applications in various fields. By mastering the "keep, change, flip" method, understanding the concept of reciprocals, and practicing regularly, you can confidently tackle fraction division problems, no matter how complex they may seem. Remember to always check your work and double-check your conversions to minimize errors. The more you practice, the more intuitive and effortless fraction division will become. This seemingly simple operation is a cornerstone of mathematical proficiency, empowering you to solve a wide range of real-world problems with precision and confidence.
Latest Posts
Latest Posts
-
How Much Fetal Fraction Is Needed For Gender
Jun 05, 2025
-
Florence Nightingale And Evidence Based Practice
Jun 05, 2025
-
Chances Of Getting Hit By A Tornado
Jun 05, 2025
-
Human Growth Hormone Frequency Hz Rats 1993
Jun 05, 2025
-
How To Get Rid Of Scars From Self Harm
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about 1 1 2 Divided By 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.