1 1/2 + 1 1/2 Cups
listenit
May 12, 2025 · 5 min read
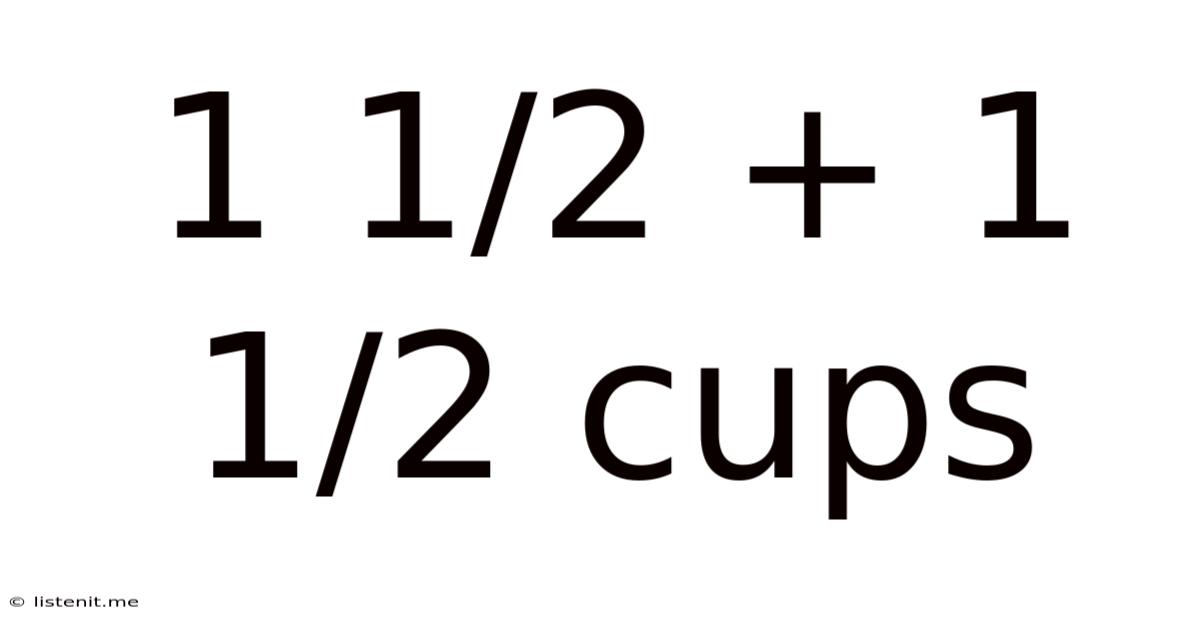
Table of Contents
Decoding the Mystery of 1 1/2 + 1 1/2 Cups: A Comprehensive Guide to Fraction Addition and Baking Success
This seemingly simple math problem, "1 1/2 + 1 1/2 cups," hides a surprisingly deep well of practical application, especially for bakers and cooks. While the answer is straightforward, understanding the underlying concepts unlocks a world of culinary confidence and precision. This guide will delve into the mathematics, practical applications, and even the potential pitfalls of adding mixed fractions in the kitchen. We'll explore various methods, offering strategies to ensure accuracy and prevent common mistakes.
Understanding Mixed Fractions: The Building Blocks of Baking
Before tackling the sum, let's break down the fundamental concept: mixed fractions. A mixed fraction combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). In our example, "1 1/2" represents one whole cup plus one-half of a cup. Understanding this structure is critical for accurate measurements.
Converting Mixed Fractions to Improper Fractions: A Key Skill
While adding mixed fractions directly is possible, converting them to improper fractions first simplifies the process considerably. An improper fraction has a numerator larger than or equal to its denominator. To convert 1 1/2 to an improper fraction:
- Multiply the whole number by the denominator: 1 * 2 = 2
- Add the numerator: 2 + 1 = 3
- Keep the same denominator: The improper fraction is 3/2.
Therefore, 1 1/2 cups is equivalent to 3/2 cups. This conversion makes adding fractions significantly easier.
Solving 1 1/2 + 1 1/2 Cups: Multiple Approaches
Now, let's explore different methods for solving 1 1/2 + 1 1/2 cups.
Method 1: Adding Improper Fractions
This is the most straightforward approach:
- Convert to improper fractions: As shown above, 1 1/2 becomes 3/2. Therefore, the problem becomes 3/2 + 3/2.
- Add the numerators: Since the denominators are the same, simply add the numerators: 3 + 3 = 6.
- Keep the same denominator: The result is 6/2.
- Simplify the fraction: 6/2 simplifies to 3.
Therefore, 1 1/2 + 1 1/2 cups = 3 cups.
Method 2: Adding Mixed Fractions Directly
While less efficient, adding mixed fractions directly is possible:
- Add the whole numbers: 1 + 1 = 2
- Add the fractions: 1/2 + 1/2 = 1
- Combine the results: 2 + 1 = 3
Again, the answer is 3 cups. This method is perfectly acceptable, especially for simple additions, but the improper fraction method is generally preferred for more complex calculations.
Method 3: Visual Representation
Visual aids, such as drawing diagrams of cups and halves, can be particularly helpful for beginners or those who prefer a more concrete understanding. Imagine two cups, each filled to the halfway point. Adding them together clearly yields three full cups.
Practical Applications in Cooking and Baking
Understanding fraction addition isn't merely an academic exercise; it's a crucial skill for anyone who enjoys cooking or baking. Precise measurements are critical to achieving the desired texture, consistency, and flavor in your culinary creations.
Baking: The Importance of Accuracy
Baking is particularly sensitive to precise measurements. A slight deviation from the recipe's instructions can significantly impact the final product. In baking, even small variations in the amount of liquid can affect the rise of the cake, the texture of the cookies, or the overall taste.
Example: Consider a recipe that calls for 1 1/2 cups of flour and 1 1/2 cups of sugar. Incorrectly measuring these ingredients could lead to a dense, dry cake, or a gooey, sticky mess. Accurate measurement using the knowledge of adding fractions is therefore crucial.
Cooking: Flexibility and Adaptation
While cooking often allows for more flexibility, understanding fraction addition still provides advantages. If a recipe calls for 1 1/2 cups of broth, but you only have 1 cup on hand, you can easily determine how much more you need (another 1/2 cup). This adaptability ensures you can still make the recipe, even with slight ingredient adjustments.
Potential Pitfalls and Common Mistakes
Even experienced bakers and cooks can fall victim to common fraction addition mistakes. Here are some to watch out for:
Forgetting to Convert to Improper Fractions
Adding mixed fractions directly without converting to improper fractions can lead to errors, especially when dealing with more complex fractions. It is highly recommended to convert to improper fractions before adding.
Incorrectly Adding Numerators and Denominators
A common mistake is adding both the numerators and the denominators. Remember, you only add the numerators when the denominators are the same; the denominator remains unchanged.
Misinterpreting the Result
After adding fractions, always check to see if the result is an improper fraction. If it is, remember to convert it back into a mixed fraction or a whole number to clearly understand the quantity.
Beyond the Basics: Expanding Your Fraction Skills
Understanding 1 1/2 + 1 1/2 cups is just the beginning. Building upon this knowledge, you can tackle more complex fraction additions in recipes.
Adding Fractions with Different Denominators
While the example above used fractions with the same denominator, many recipes involve fractions with different denominators. To add these, you must first find a common denominator—a number that is a multiple of both denominators. For example, to add 1/3 + 1/4, you would find a common denominator of 12, converting the fractions to 4/12 and 3/12, respectively.
Multiplying and Dividing Fractions
Beyond addition, understanding fraction multiplication and division is important for scaling recipes up or down. These operations are crucial for adapting recipes to larger or smaller quantities of servings. Recipes often call for doubling or halving ingredients, requiring proficiency in fraction manipulation.
Mastering Fraction Conversions
Fluency in converting between fractions, decimals, and percentages is also highly beneficial for cooking and baking. Some recipes may list measurements in decimal form (e.g., 1.5 cups), while others may use percentages. Converting between these forms allows for seamless recipe interpretation and modification.
Conclusion: Precision and Confidence in the Kitchen
Mastering the seemingly simple calculation of 1 1/2 + 1 1/2 cups unlocks a world of culinary confidence and precision. By understanding the underlying principles of fraction addition, converting mixed fractions to improper fractions, and avoiding common pitfalls, you'll be well-equipped to confidently tackle any recipe, ensuring delicious and consistent results every time. Embrace the math, and enjoy the rewards in your culinary adventures!
Latest Posts
Latest Posts
-
Oxidation Number Of Cr In K2cr2o7
May 12, 2025
-
Matter Is Anything That Has And Takes Up
May 12, 2025
-
When Do Parentheses Appear In The Formulas Of Ionic Compounds
May 12, 2025
-
What Percentage Of 20 Is 1
May 12, 2025
-
What Is 28 In A Fraction
May 12, 2025
Related Post
Thank you for visiting our website which covers about 1 1/2 + 1 1/2 Cups . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.