0.85 As A Fraction In Simplest Form
listenit
Apr 04, 2025 · 5 min read
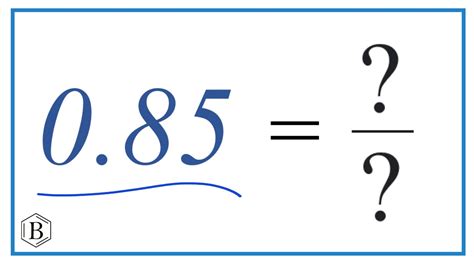
Table of Contents
0.85 as a Fraction in Simplest Form: A Comprehensive Guide
Converting decimals to fractions is a fundamental skill in mathematics, crucial for various applications from basic arithmetic to advanced calculus. This comprehensive guide delves into the process of converting the decimal 0.85 into its simplest fractional form, providing a detailed explanation and exploring related concepts. We'll not only show you how to do it but also why the method works, ensuring a thorough understanding of the underlying principles.
Understanding Decimals and Fractions
Before we jump into the conversion, let's briefly review the concepts of decimals and fractions. Decimals represent numbers as a sum of powers of 10, using a decimal point to separate the whole number part from the fractional part. Fractions, on the other hand, represent a part of a whole, expressed as a ratio of two integers: a numerator (top number) and a denominator (bottom number).
The decimal 0.85 represents eighty-five hundredths, meaning 85 parts out of 100. This inherent relationship between decimals and fractions provides the foundation for our conversion.
Converting 0.85 to a Fraction: Step-by-Step
The conversion process is straightforward and involves these steps:
1. Write the decimal as a fraction over 1:
This is the initial step. We write 0.85 as a fraction by placing it over the denominator 1:
0.85/1
2. Eliminate the decimal point by multiplying both the numerator and the denominator by a power of 10:
Since 0.85 has two digits after the decimal point, we multiply both the numerator and denominator by 10². This effectively shifts the decimal point two places to the right, removing it entirely.
(0.85 x 100) / (1 x 100) = 85/100
This gives us the fraction 85/100. This fraction represents the same value as 0.85.
3. Simplify the Fraction:
Now, we need to simplify the fraction 85/100 to its simplest form. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD).
To find the GCD of 85 and 100, we can use several methods. One common approach is to find the prime factorization of both numbers:
- Prime factorization of 85: 5 x 17
- Prime factorization of 100: 2 x 2 x 5 x 5 = 2² x 5²
The greatest common divisor is the product of the common prime factors raised to their lowest power. In this case, the only common prime factor is 5, and its lowest power is 5¹. Therefore, the GCD of 85 and 100 is 5.
Now we divide both the numerator and denominator by 5:
85 ÷ 5 = 17
100 ÷ 5 = 20
This simplifies the fraction to its simplest form: 17/20
Therefore, 0.85 as a fraction in its simplest form is 17/20.**
Understanding the Simplification Process: A Deeper Dive
The process of simplifying fractions is essential for representing numbers in their most concise and efficient form. It's not just about aesthetics; it simplifies calculations and improves understanding. Here's a more in-depth look at the simplification process:
-
Greatest Common Divisor (GCD): Finding the GCD is the key to simplifying fractions. The GCD represents the largest number that divides both the numerator and denominator without leaving a remainder. Methods for finding the GCD include prime factorization (as demonstrated above), the Euclidean algorithm (a more efficient method for larger numbers), and using readily available online GCD calculators.
-
Prime Factorization: This method breaks down a number into its prime factors – numbers divisible only by 1 and themselves. This provides a clear view of the components of a number, making it easier to identify common factors.
-
Euclidean Algorithm: This algorithm is a more efficient method for finding the GCD of larger numbers. It involves a series of divisions until the remainder is zero. The last non-zero remainder is the GCD.
Applications of Decimal-to-Fraction Conversion
Converting decimals to fractions has numerous applications across various fields:
-
Basic Arithmetic: Adding, subtracting, multiplying, and dividing fractions is sometimes easier than working with decimals, especially when dealing with complex fractions.
-
Algebra: Many algebraic equations and expressions involve fractions, requiring a thorough understanding of their manipulation.
-
Geometry and Measurement: Calculations involving areas, volumes, and angles frequently utilize fractions.
-
Chemistry and Physics: Many scientific formulas and calculations rely on fractions to represent ratios and proportions.
-
Computer Programming: Representing numerical values in programs often necessitates converting between decimals and fractions.
Further Exploration: Working with More Complex Decimals
While 0.85 is a relatively simple decimal to convert, the same principles apply to more complex decimals, including those with repeating or non-terminating decimal expansions. For example:
-
Terminating Decimals: These decimals have a finite number of digits after the decimal point. The conversion process remains the same; multiply by the appropriate power of 10 and simplify.
-
Repeating Decimals: These decimals have a sequence of digits that repeat infinitely. Converting these requires a slightly different approach, involving algebraic manipulation to solve for the fractional representation.
Conclusion
Converting 0.85 to its simplest fractional form, 17/20, is a straightforward process that highlights the fundamental relationship between decimals and fractions. Understanding this conversion, along with the underlying concepts of simplification and finding the greatest common divisor, provides a strong foundation for working with numbers in various mathematical contexts. This skill is invaluable for students and professionals alike, extending beyond basic arithmetic to more advanced mathematical applications. Mastering this skill empowers you to confidently navigate numerical problems and appreciate the elegance and practicality of mathematical principles.
Latest Posts
Latest Posts
-
How Much Does A Dozen Golf Balls Weigh
Apr 04, 2025
-
What Is The Highest Common Factor Of 12 And 4
Apr 04, 2025
-
How Many Protons Neutrons Electrons Does Sulfur Have
Apr 04, 2025
-
Is Air A Element Or Compound
Apr 04, 2025
-
What Is 40 Percent Of 5000
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about 0.85 As A Fraction In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
